![Dynamische Investitionsrechnung: Kapital- und Endwerte]()
Mit Investitionsrechnungen will ein Unternehmen oder auch eine Privatperson ermitteln, ob eine
Handlungsmöglichkeit (Projekt, Alternative, Investition usw.) vorteilhaft ist. Die Verfahren der
Investitionsrechnung werden üblicherweise in statische und dynamische Verfahren eingeteilt.
Die Grundlagen, Verfahren, Probleme und Verbesserungsmöglichkeiten der
statischen Rechnung finden sich in den folgenden Beiträgen:
Aufgrund der zahlreichen Kritikpunkte wird immer mehr der Einsatz der
dynamischen Verfahren empfohlen, die zwar etwas arbeitsaufwändiger sind, aber auch viele Probleme lösen. Die Grundlagen finden sich im Beitrag "Grundlagen des dynamischen Investitionsrechnung".
Als Ergebnis der in dem Beitrag beschriebenen Vorarbeiten (insb. der
intraperiodischen Verzinsung) liegt eine modifizierte Zahlungsreihe vor, welche die folgende zeitliche Struktur aufweist:
 Abb. 1: Zahlungsstrom entsprechend dem Zeitkonzept
Abb. 1: Zahlungsstrom entsprechend dem Zeitkonzept
Es sei wegen der Wichtigkeit wiederholt darauf hingewiesen, dass die Zahlungen und Zahlungsänderungen (jeweils im Vergleich zur Nullalternative) immer nur für ein
Szenario gelten. Daher müssen in weiteren Schritten auch andere wichtige
Szenarien beachtet werden.
Da die Zahlungen an unterschiedlichen Zeitpunkten anfallen (im Beispiel der Abb. 1 von t = 0 bis t = tn = 4), können sie nicht direkt verglichen werden. Es müssen
einheitliche Vergleichszeitpunkte bestimmt werden. Die erste Möglichkeit besteht im Kapitalwertkriterium, welches wie das Endwertkriterium zu den
absoluten Verfahren (im Unterschied zu den relativen = Kapitalrenditen) gehört.
Kapitalwerte
Der
Entscheidungsträger kann vorgeben, zu welchem Zeitpunkt der Vergleich durchgeführt werden soll. Die einzige Vorgabe, die er einhalten muss, ist die, dass es sich um einen einheitlichen Vergleichszeitpunkt für alle Handlungsmöglichkeiten und alle Szenarien handeln muss.
Er kann somit im ersten Schritt jeden
Vergleichszeitpunkt wählen, also auch den Startzeitpunkt oder den Endzeitpunkt der Handlungsmöglichkeit oder sogar die Jahrtausendwende oder den 22.2.2222. Solange einheitliche Zins- und Steuersätze gelten und kein Kapitalmangel vorliegt, ergibt sich immer die gleiche Vorteilhaftigkeitsreihenfolge.
Allerdings ist der
Arbeitsaufwand bei ungewöhnlichen Vergleichszeitpunkten zu berücksichtigen, wozu dann teilweise noch Schwierigkeiten bei der
Interpretierbarkeit der Ergebnisse kommen. Insofern wird neben dem Endzeitpunkt der Investition meistens nur noch der Startzeitpunkt als Alternative betrachtet (Kapitalwertkriterium).
Das
Kapitalwertkriterium wird in der Praxis und auch in der Theorie intensiv eingesetzt, so dass es als erstes vorgestellt wird. Da bei der Kapitalwertmethode der Startzeitpunkt (t = 0) der Vergleichszeitpunkt ist, müssen alle Zahlungen und Zahlungsänderungen auf diesen Zeitpunkt abgezinst werden, was die folgende Abb. 2 für den oben aufgeführten Zahlungsstrom zeigt:
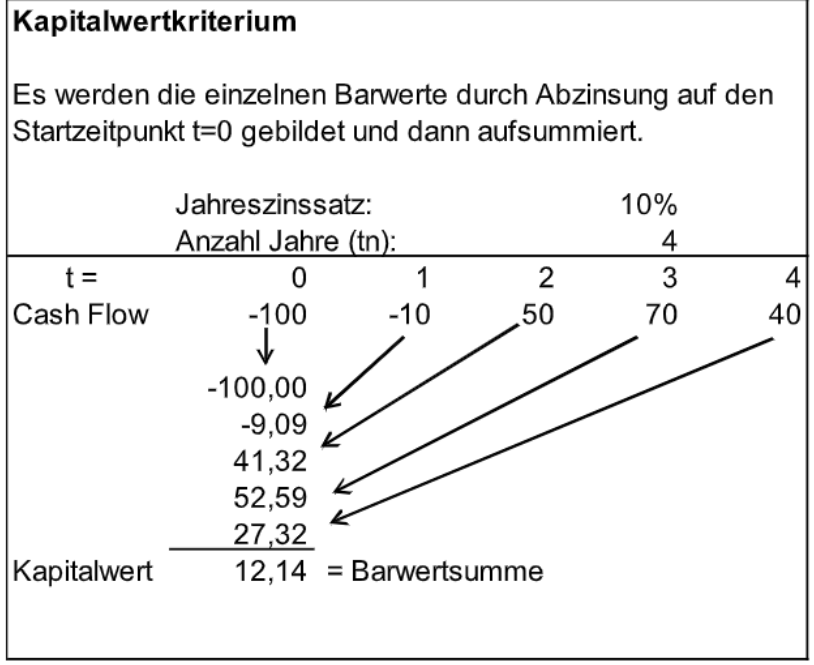 Abb. 2: Kapitalwertberechnung für den Zahlungsstrom
Abb. 2: Kapitalwertberechnung für den Zahlungsstrom
Die
Anfangsauszahlung von – 100 T€
0 kommt bereits zum Vergleichszeitpunkt in t = 0, so dass eine Abzinsung nicht notwendig ist. Die
Währungseinheiten tragen zur höheren Präzision einen Zeitindex (vgl. zu dieser erweiterten Schreibweise Hoberg (2018), S. 468 ff.).
Der
Überschuss von – 10 T€
1 zum Zeitpunkt t = 1 fällt ein Jahr später an, so dass eine einjährige Abzinsung (Division durch 1 + Jahreszinssatz) erfolgen muss (
Barwertbildung). Es ergibt sich für t = 0 ein Barwert von – 10/1,1 = – 9,09 T€
0 (siehe auch Abb. 2). Die Abzinsungen werden auch für die weiteren Zahlungen vorgenommen.
Die letzte Zahlung in t = tn = 4 muss über 4 Perioden abgezinst werden: 40 T€
4 / (1,14 T€
4 / T€
0) = 27,32 T€
0. Dann können die einzelnen Barwerte zum Kapitalwert addiert werden, was einen positiven Wert von 12,14 T€
0 ergibt. Die einzelnen
Rechenoperationen sollen auch in der folgenden Abbildung mit dem Ausweis der individuellen und kumulierten Barwerte deutlich gemacht werden. Das Ergebnis ist natürlich identisch:
|
Kalkulationszinssatz
|
10 % p.a.
|
|
Zeitpunkte t =
|
0
|
1
|
2
|
3
|
4
|
|
|
Einheit
|
|
|
|
|
|
|
Zahlungsstrom
|
T€t
|
–100,0
|
–10,0
|
50,0
|
70,0
|
40,0
|
|
Barwerte
|
T€0
|
–100,0
|
–9,1
|
41,3
|
52,6
|
27,3
|
|
kumuliert
|
T€0
|
–100,0
|
–109,1
|
–67,8
|
–15,2
|
12,1
|
|
Kapitalwert (= Barwertsumme):
|
12,1 T€0
|
Abb. 3: Kapitalwertermittlung für die Beispielsdaten
In der letzten Zeile sind auch die
kumulierten Barwerte angegeben. Sie zeigen, dass erst nach gut 3,5 Jahren positive Werte erreicht werden. Und erst dann ist die Handlungsmöglichkeit für das betrachtete Szenario vorteilhaft. Formelmäßig ergibt sich der
Kapitalwert wie folgt (vgl. z. B. Götze, S. 78 ff. oder Varnholt/Hoberg/Wilms/Lebefromm, S. 59 ff.):
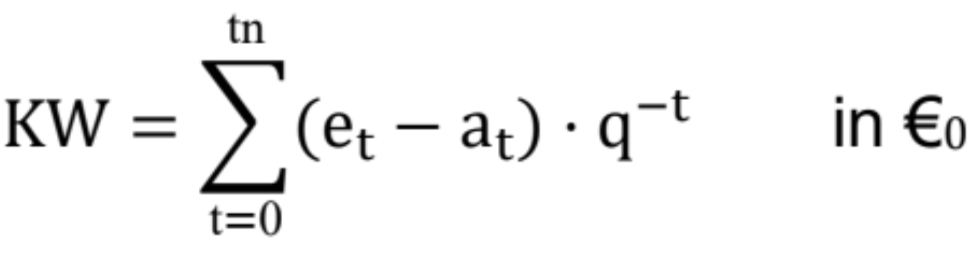
KW
|
Kapitalwert zum Zeitpunkt t = 0 in €0
|
et
|
Einzahlungen zum Zeitpunkt t in €t
|
at
|
Auszahlungen zum Zeitpunkt t in €t
|
|
q
|
Jahreszinsfaktor = 1 + i
|
|
i
|
Jahreszinssatz
|
|
t
|
Zeitindex, t = 0…tn
|
Die Anwendung der
Kapitalwertformel führt selbstverständlich zu den gleichen Ergebnissen wie in den obigen Abbildungen. Für die endgültige
Entscheidung über die Vorteilhaftigkeit einer Handlungsmöglichkeit ist es nun wichtig, auch alternative Zahlungsströme aus anderen Szenarien zu analysieren (vgl. Hoberg (2017), S. 22 ff.). Insbesondere sollten
Maximalgefahren betrachtet werden.
Dies hat die Bayer AG wohl nicht im hinreichenden Ausmaß durchgeführt, als sie den
Skandalkonzern Monsanto gekauft hat. Nur wenn die Handlungsmöglichkeit auch in schlechten Szenarien beherrschbar bleibt, sollten
positive Durchführungsentscheidungen getroffen werden. Der Kapitalwert (= Überschuss per t = 0) lässt sich nicht einfach interpretieren.
Eine Möglichkeit besteht in der Aussage, dass der Kapitalwert angibt, um welchen Betrag sich der heutige Wert des Unternehmens erhöht, wenn eine
positive Entscheidung fällt und das Szenario dann auch wie angenommen eintritt.
Endwertkriterium
Während der Kapitalwert den Wert zum Startzeitpunkt angibt, wird mit dem Endwert der Wert zum Endzeitpunkt (t = tn) ermittelt. Denn es kommt häufig vor, dass der
Entscheidungsträger zum Ende des Projektes einen möglichst hohen Überschuss erzielen möchte. Diese Interpretation ist leicht nachvollziehbar. Man will wissen, welchen Nutzen eine Handlungsmöglichkeit am Ende bringen wird.
Für die Ermittlung des Endwertes sind alle
Ein- und
Auszahlungen auf den einheitlichen Vergleichszeitpunkt des Projektendes (t = tn) zu beziehen, indem sie entsprechend aufgezinst werden. Im Beispiel läuft die Handlungsmöglichkeit über 4 Jahre (tn = 4). Um den Endwert zu berechnen, wird jede einzelne Zahlung entsprechend ihrem Abstand zum Endzeitpunkt (im Beispiel t = tn = 4) hochgezinst.
Es werden also die
Einzelendwerte gebildet. Somit muss eine Zahlung, die in t = 1 anfällt, über 3 Jahre aufgezinst werden. Durch die Addition aller Einzelendwerte entsteht der gesamte Endwert. Die Anwendung auf die Beispielsdaten ergibt:
 Abb. 4: Beispiel für das Endwertkriterium (eigene Darstellung)
Abb. 4: Beispiel für das Endwertkriterium (eigene Darstellung)
Die Abb. 4 zeigt, wie zunächst die einzelnen Endwert einer jeden Zahlung gebildet werden, indem eine
Aufzinsung auf den Vergleichszeitpunkt t = 4 stattfindet. Die aufgezinsten Größen haben dann die Einheit T€
4, was besagt, dass der Betrag auf den Zeitpunkt 4 bezogen ist und auch dessen Kaufkraft besitzt. Die
Anschaffungsauszahlung von –100 T€
0 wird durch die Multiplikation mit 1,14 = 1,4641 auf den Zeitpunkt t = 4 bezogen, wodurch ein Einzelendwert von –146,21 T€
4 entsteht.
Genauso werden die weiteren Zahlungen
hochgezinst. Der
Gesamt-Endwert entsteht dann dadurch, dass die einzelnen Endwerte aufsummiert werden. Dies ist erst zulässig, wenn alle Zahlungen auf den Zeitpunkt t = 4 bezogen sind. Die gleichen Ergebnisse wie in Abb. 4 erhalten wir auch, wenn wieder eine Tabelle aufgebaut wird; dieses Mal für die Endwerte:
|
Kalkulationszinssatz
|
10 % p.a.
|
|
Zeitpunkte t =
|
0
|
1
|
2
|
3
|
4
|
|
|
Einheit
|
|
|
|
|
|
|
Zahlungsstrom
|
T€t
|
–100,0
|
–10,0
|
50,0
|
70,0
|
40,0
|
|
Einzelendwerte
|
T€4
|
–146,4
|
–13,3
|
60,5
|
77,0
|
40,0
|
|
kumulierte Ews
|
T€4
|
–146,4
|
–159,7
|
–99,2
|
–22,2
|
17,8
|
|
Kapitalwert (= Barwertsumme):
|
17,8 T€4
|
Abb. 5: Endwertermittlung für die Beispieldaten
Für die
Beispielsdaten resultiert der
positive Endwert von 17,8 T€4. Dies zeigt, dass sich die Handlungsmöglichkeit im betrachteten Szenario lohnt, weil alle Auszahlungen gedeckt sind und am Ende des vierten und letzten Jahres noch dieser Betrag von 17,8 T€
4 zur Entnahme übrig bleibt. Die Formel für die Endwertberechnung lautet wie folgt:
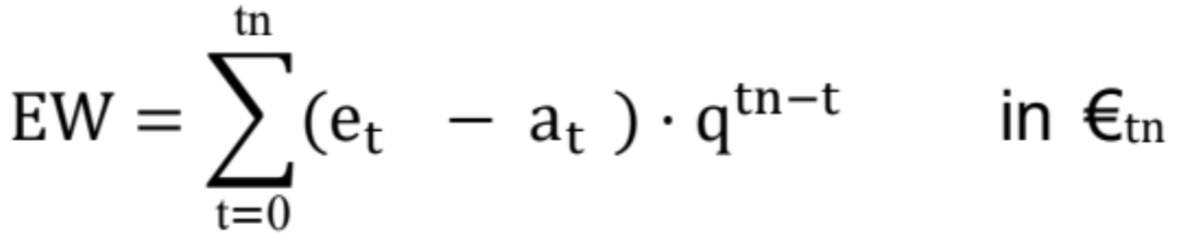
EW Endwert: Summe aller Einzelendwerte in T€
4
Das Endwertkriterium führt somit zum gleichen positiven Ergebnis wie die Kapitalwertmethode, wobei sich die Differenz im Betrag ausschließlich auf die unterschiedlichen
Bezugszeitpunkte zurückführen läßt. Denn bei gleichen Zinssätzen und unbegrenzten Möglichkeiten der Kreditaufnahme lassen sich Kapitalwert und Endwert im Falle der Berechnung
ohne Ertragsteuern mittels einfacher Aufzinsung ineinander überführen.
Es gilt folgende
Beziehung:
EW = KW × qtn = 12,14 × 1,4641 = 17,78 T€4
Diese Übereinstimmung lässt sich auch für alle anderen einheitlichen Vergleichszeitpunkte zeigen. Wegen der besseren Interpretierbarkeit empfiehlt sich jedoch die Endwertmethode. Eine
alternative Darstellung könnte man in den
Annuitäten sehen. Sie werden berechnet, indem z. B. der Kapitalwert verzinslich auf die Jahre verteilt wird (vgl. zu dieser Methode Hoberg (2020), S. 1 ff.).
Damit kann der
jährliche Einfluss der Handlungsmöglichkeit dargestellt werden. Aber auch jede andere zeitliche Struktur der Zahlungsüberschüsse, die ein Investor anstrebe möge, kann errechnet werden. Insgesamt kann festgehalten werden, dass die absoluten Kriterien wie Kapitalwert oder Endwert gut geeignet zur Bewertung sind, solange genügend
Kapital vorhanden ist.
Literaturverzeichnis
- Götze, U.: Investitionsrechnung: Modelle und Analysen zur Beurteilung von Investitionsvorhaben, 7. Auflage, Berlin, Heidelberg, New York 2014.
- Hoberg, P. (2015): Restwerte in der Investitionsrechnung, in: Wisu 7/2015, 44. Jg., S. 1337-1342.
- Hoberg, P. (2017): Die Szenarientechnik in der BWL, in: Controlling-Journal, Heft 4/2017, S. 22-26. Hoberg, P. (2018): Einheiten in der Investitionsrechnung, in: WISU, 47. Jg., 4/2018, S. 468-474.
- Hoberg, P. (2020): Controllers Trickkiste: Die sichere Auswahl von finanzmathemati-schen Faktoren, in: https://www.controllingportal.de/Fachinfo/Investitionsrechnung/Controllers-Trickkiste-Die-sichere-Au..., 8.5.2020.
- Hoberg, P. (2023): Bericht aus der Praxis: Fortgeführte Nullalternative bei Investitionen, 12.4.2023.
- Varnholt, N., Hoberg, P., Wilms, S., Lebefromm, U.: Investitionsmanagement - Betriebswirtschaftliche Grundlagen und Umsetzung mit SAP®S/4HANA, Berlin/Boston 2023.
letzte Änderung P.D.P.H.
am 03.06.2025
Autor:
Prof. Dr. Peter Hoberg
|
Autor:in
 |
Herr Prof. Dr. Peter Hoberg
Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung.
|
|
weitere Fachbeiträge des Autors
| Forenbeiträge
|


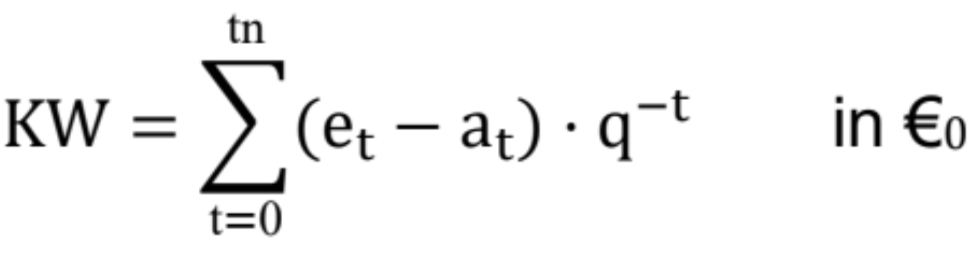










 In dieser Position unterstützen Sie aktiv die finanzielle Steuerung und Transparenz unseres Werks, leisten einen wichtigen Beitrag zu fundierten Managemententscheidungen und tragen zur wirtschaftlichen Weiterentwicklung des Standorts bei – mit attraktiven Möglichkeiten zur fachlichen und persönli... Mehr Infos >>
In dieser Position unterstützen Sie aktiv die finanzielle Steuerung und Transparenz unseres Werks, leisten einen wichtigen Beitrag zu fundierten Managemententscheidungen und tragen zur wirtschaftlichen Weiterentwicklung des Standorts bei – mit attraktiven Möglichkeiten zur fachlichen und persönli... Mehr Infos >>
 Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
 Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
 Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
 Wir, die Gubor-Gruppe, gehören als erfolgreiches, familiengeführtes Unternehmen mit rund 1.500 Mitarbeitern europaweit zu den Marktführern von Süßwarenartikeln. Unsere Produkte fertigen wir an fünf Standorten in Deutschland sowie einem Standort in Polen. Dabei setzen wir sowohl in der Beschaffung... Mehr Infos >>
Wir, die Gubor-Gruppe, gehören als erfolgreiches, familiengeführtes Unternehmen mit rund 1.500 Mitarbeitern europaweit zu den Marktführern von Süßwarenartikeln. Unsere Produkte fertigen wir an fünf Standorten in Deutschland sowie einem Standort in Polen. Dabei setzen wir sowohl in der Beschaffung... Mehr Infos >>
 Die Fraunhofer-Gesellschaft (www.fraunhofer.de) ist eine der weltweit führenden Organisationen für anwendungsorientierte Forschung. 75 Institute entwickeln wegweisende Technologien für unsere Wirtschaft und Gesellschaft – genauer: 32 000 Menschen aus Technik, Wissenschaft, Verwaltung und... Mehr Infos >>
Die Fraunhofer-Gesellschaft (www.fraunhofer.de) ist eine der weltweit führenden Organisationen für anwendungsorientierte Forschung. 75 Institute entwickeln wegweisende Technologien für unsere Wirtschaft und Gesellschaft – genauer: 32 000 Menschen aus Technik, Wissenschaft, Verwaltung und... Mehr Infos >>
 Die WIRTGEN GROUP ist ein international führender Unternehmensverbund der Baumaschinenindustrie mit rund 9.000 Beschäftigten weltweit. Als starker Teil von John Deere und mit unseren spezialisierten Marken WIRTGEN, VÖGELE, HAMM, KLEEMANN, BENNINGHOVEN, CIBER sowie Werken in Deutschland, Brasilien... Mehr Infos >>
Die WIRTGEN GROUP ist ein international führender Unternehmensverbund der Baumaschinenindustrie mit rund 9.000 Beschäftigten weltweit. Als starker Teil von John Deere und mit unseren spezialisierten Marken WIRTGEN, VÖGELE, HAMM, KLEEMANN, BENNINGHOVEN, CIBER sowie Werken in Deutschland, Brasilien... Mehr Infos >>
 Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>







 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>