Preispolitik bei steigenden Kosten - Preiserhöhungen ohne Preiserhöhungen

Die Preise haben eine überragende Bedeutung für die Gewinne der Unternehmen. Dies gilt für beide Richtungen. Insofern sollten die Unternehmen im Wettbewerbsumfeld sorgfältig analysieren, wie sich eventuelle Preisänderungen auswirken würden. Die Controller sind immer dann besonders gefordert, wenn sich die Bedingungen auf dem Absatz- und/oder Beschaffungsmarkt wesentlich ändern. Gerade seit dem Herbst 2021 mit den schnell steigenden Preisen insbesondere bei Rohstoffen steht die Notwendigkeit von Preiserhöhungen im Mittelpunkt. So lassen steigende Energiekosten, die sich teilweise mehr als verdoppelt haben (Ölpreise von 39 auf 85 US-Dollar pro Barrel), die Margen schmelzen. Da praktisch alle Branchen von den Energiepreiserhöhungen betroffen sind, werden auch Unternehmen Preise erhöhen wollen, die nicht im Energiesektor arbeiten. Sie wollen ihre erhöhten Kosten auf die Kunden abwälzen.

Bei sich verdoppelnden Kosten für einige Energiearten besteht aus volkswirtschaftlicher Sicht die Gefahr, dass sich die Verbraucher an die Preissteigerungen gewöhnen. Umgekehrt kann es sein, dass die Monatsbudgets der Verbraucher durch die gestiegenen Energiepreise so belastet werden, dass sie in anderen Warengruppen noch preisbewusster werden (müssen). Preissteigerungen sind verpönt, was sowohl für den Handel als auch für die Verbraucher gilt. In jedem Fall ist es für Unternehmen ohne monopolartige Stellung nicht einfach, die Preise zu erhöhen. Teilweise werden sie vom Handel auch an den Pranger gestellt, indem an den leeren Regalen zu lesen ist, dass man im Interesse der Kunden die "unverschämten" Preiserhöhungen nicht akzeptieren will. So hat Kaufland 2018 fast das ganze Sortiment von Unilever ausgelistet mit Ausnahme der Eismarken (HB vom 21.12.2018).

Insofern sind offizielle Preiserhöhungen nur selten durchführbar, und auch nicht jedes Jahr. Einfacher hat es die Post, welche einfach Kostensteigerungen angeben kann, um das Porto wieder zu erhöhen. Aber so eine starke Marktstellung haben nur die wenigsten Unternehmen. Daher sollten Unternehmen versuchen, die Netto-Preise auch ohne offizielle Preiserhöhung zu steigern. Das Controlling spielt bei den dafür notwendigen Kalkulationen eine besondere Rolle.

1. Grundlagen Preispolitik

Preise sind häufig das mächtigste Instrument zur Erhöhung der Gewinne eines Unternehmens (vgl. z. B. Simon/Fassnacht, S. 1 ff.). Umgekehrt kann ein Unternehmen mit einer schlechten Preispolitik seinen Untergang herbeiführen. Die Absatzmengen lassen sich durch den Einsatz der Preispolitik auch kurzfristig beeinflussen. Unternehmen versuchen, z. B. mit dem Einsatz bewährter Marken, eine hohe Preisbereitschaft in den Zielgruppen zu erreichen (vgl. z. B. Hünerberg, S. 13 ff.).

Die erwarteten Verkaufsmengen eines Produktes lassen sich als Antwort des Marktes auf den Marketingmix des Unternehmens verstehen, wobei auch die weiteren Einflussgrößen des Umfelds im weiteren Sinne zu beachten sind. Insb. die Reaktion der Konkurrenz auf den Marketingmix des Unternehmens muss antizipiert werden, was aber nur selten richtig geschieht (vgl. hierzu Hoberg (2017), S. 30 ff.). Bezogen auf den Preis des Konkurrenzproduktes kann versucht werden, mit der Kreuzpreiselastizität den Einfluss zu bestimmen (vgl. z. B. Homburg. S. 685 ff.).

In der Frage nach der optimalen Preis-Mengen-Kombination kann das Unternehmen nur über die Preise im weiten Sinne entscheiden, wobei im Falle der Einschaltung von Absatzmittlern wie den Handelsketten nur die Preise an diese Mittler festgelegt werden können. Eine Preisbindung für den Endkunden ist nicht zulässig. Bei zu hohen Preisen werden die Mengen bescheiden bleiben. Zu niedrige Preise hingegen sind zwar häufig gut für die Mengen, aber nicht für die Margen, so dass schnell die Gewinne des Unternehmens erodieren können. Insofern muss sorgfältig analysiert, welches die richtigen Preise für die Endkunden bzw. für die Absatzmittler sind.

1.1 Preisabsatzfunktionen

Die Standardantwort der Betriebswirtschaftslehre auf die Frage nach der besten Preissetzung beinhaltet im ersten Schritt die Nutzung von Preisabsatzfunktionen (PAF), welche für jede Preissetzung angeben, wie hoch die resultierende Menge voraussichtlich sein wird (vgl. z. B. Wöhe, S. 412 ff., Hoberg (2018), S. 1937 ff.). Teilweise werden auch Elastizitäten eingesetzt, welche die relative Mengenänderung in Abhängigkeit der relativen Preisänderungen angeben (Vgl. auch zu den Problemen Hoberg (2013), S- 320). Wie oben angeführt muss die Mengenschätzung auch die antizipierte Reaktion anderer Marktteilnehmer (insb. Konkurrenz) beinhalten.

Für die Nutzung dieses Standardmodells sind einige Präzisierungen notwendig. Insbesondere sei darauf hingewiesen, dass der Preis immer der Nettopreis sein muss, also nach Berücksichtigung aller Rabatte (in der Rechnung, auf den Rechnungsbetrag und Rückvergütungen) und der Effekte der Zahlungsziele (vgl. Varnholt/Lebefromm/Hoberg, S. 126 ff.). In der Literatur wird die Wirkung der verschiedenen Rabatte als "Price Waterfall" Zahlungszielen und die Nachteile aufgrund von subventionierten Krediten (z. B. 0 %-Kredite).

Im Folgenden wird der Preis daher als Nettopreis p_N angegeben, um deutlich zu machen, dass wirklich alle Erlösschmälerungen inklusive eventueller Finanzierungskosten abgezogen sein müssen. Zudem sei auf die Notwendigkeit hingewiesen, die zu betrachtende Periode genau festzulegen. Denn die Wirkungsbeziehungen können sich schon wenig später ändern, was insb. für Produkte gilt, deren Nachfrage von der Saison abhängt.

Es ist offensichtlich, dass höhere Preise bis auf wenige Sonderfälle zu niedrigeren Mengen führen und vice versa. Daher weist die Preisabsatzfunktion (PAF) eine negative Steigung auf. Die PAF wird üblicherweise linear angenommen, was weiter unten noch diskutiert wird. Sie stellt das Ergebnis der Entscheidung von sehr vielen Kunden dar und ist somit das Ergebnis der Aggregation von vielen Einzelentscheidungen. Die PAF beginnt mit dem Prohibitivpreis p_PH für eine Menge von 0 (Schnittpunkt auf der Y-Achse). In ihrer linearen Variante hat die Preisabsatzfunktion das folgende Aussehen:

pN	Nettopreis in GE/ME
pPH	Prohibitivpreis in GE/ME
a	Steigungsparameter, üblicherweise negativ
x	Fakturierte Menge in ME/Pe
UG	Untergrenze der fakturierbaren Mengen in ME/Pe
OG	Obergrenze der fakturierbaren Mengen in ME/Pe

Es ist sinnvoll, die Gültigkeit der Preisabsatzfunktion einzugrenzen, weil bei extremen Werten für die Absatzmengen häufig keine lineare Funktion mehr vorliegt oder weil Unstetigkeitsstellen berücksichtigt werden müssen (vgl. Hoberg (2018b), S. 1937 ff.). Am Rande sei bemerkt, dass hier die übliche Schreibweise gewählt wurde mit x als unabhängiger Variable, was eigentlich nicht korrekt ist, da das Unternehmen nur die Preise (teilweise) beeinflussen kann. Das würde dann auch bedeuten, dass die Ober- und Untergrenzen für die Preise gesetzt werden müssten. Aber wenn man diesen Hintergrund im Kopf hat, reicht auch die übliche einfachere Darstellung. Die Einfachheit resultiert daraus, dass die Kostenfunktion die Menge als unabhängige Variable aufweist, so dass dann leichter Deckungsbeitrags- und Gewinnfunktionen gebildet werden können.

Die Zusammenhänge seien anhand eines Beispiels dargestellt. Der Prohibitivpreis betrage in der betrachteten Periode 14,50 €/ME und die Steigung a -0,0001. Diese Parameter schätzt das Unternehmen auf der Basis von Marktforschungen. Es wird für verschiedene Preissetzungen prognostiziert, welche Menge in der betrachteten Periode resultieren würde. Aus den Punkten werden dann die Parameter Prohibitivpreis und Steigung der – in diesem Falle linear unterstellten – Preisabsatzfunktion bestimmt. Sie gilt nur in bestimmten Intervallen. Im Beispiel sei sie nur für Mengen zwischen 15.000 und 40.000 ME/Pe:

p_N = 14,5 - 0,0001 * x in €/ME mit 15.000 <= x <= 45.000 ME/Pe

Bei einem Prohibitivpreis von p_PH = 14,5 €/ME ist laut den Parametern dieser Preisabsatzfunktion ein Preisniveau erreicht, bei dem niemand mehr kauft. Für jede Mengeneinheit, die das Unternehmen nun absetzen will, muss es den Nettopreis jeweils um 0,0001 €/ME reduzieren. Wenn es schließlich 145.000 ME/Pe verkaufen will (außerhalb des Gültigkeitsbereichs), müsste es den Preis auf 14,5 – 0.0001 * 145.000 = 0 senken. Die bei diesem Preis von 0 absetzbare Menge wird Sättigungsmenge genannt.

Es sei darauf hingewiesen, dass diese Arten von Preisabsatzfunktionen einige Probleme aufweisen (vgl. dazu Hoberg (2018), S. 1937 ff.). Für die Zwecke dieser Untersuchung sind sie nicht so wesentlich, zumal auch nur ein begrenztes Preisintervall zwischen 15.000 und 45.000 ME/Pe betrachtet werden soll. An den Rändern - also bei extremen Preisen - tauchen häufiger Abweichungen auf, so dass die Funktion nur für diesen mittleren Bereich als relevant definiert sei.

1.2 Optimale Preis-Mengen-Kombination

Die Zielgröße besteht im Gewinn der betrachteten Periode. Die Einflüsse auf folgende Perioden seien ausgeklammert. Für die Optimierung wird noch der Grenzkostensatz benötigt, welcher durchgängig mit 6,5 €/ME angenommen wird. Es gilt somit die Linearitätsannahme (vgl. Varnholt/Hoberg/Gerhards/Wilms/Lebefromm), S. 423 ff.). Degressionseffekte im Stückkostensatz, z. B. aufgrund höherer Einkaufsmengen, seien somit nicht betrachtet.

Die Fixkosten für Verwaltung, Mieten, Produktentwicklung, PR, Zentralfunktionen, zeitlich bedingten Abschreibungen usw. ändern sich in der betrachteten Periode nicht, so dass sie bei der Optimierung herausfallen werden. Unter diesen Annahmen kann die Gewinnfunktion G wie folgt aufgestellt werden:

G	Gewinn in der betrachteten Periode in GE/Pe
kv	Variabler Stückkostensatz in €/ME
Kfix	Periodenfixkosten in €/Pe

Nach Ableitung der Gewinnfunktion und Nullsetzung erhält man (vgl. ausführlicher zu den Arbeitsschritten Hoberg (2013), S. 322 ff.):

xopt	Gewinnoptimale Menge in ME/Pe

Diese Bedingung für das Mengenoptimum wird in die PAF eingesetzt. Nach Umformung ergibt sich:

Popt	Gewinnoptimaler Preis in €/ME

Mit den obigen Daten ergibt sich der optimale Preis zu (14,5 + 6,5) / 2 = 10,5 €/ME bei einer optimalen Menge von (14,5 – 6,5) / (-2* -0,0001) = 40.000 ME/Pe. Die optimale Menge liegt somit im zulässigen Intervall von 15.000 bis 45.000. Mit dieser Vorgehensweise kann nun jedes Produkt analysiert werden. Bevor die Ergebnisse jedoch in die Praxis übertragen werden können, muss der Nettopreis zurückgerechnet werden in den Listenpreis unter Berücksichtigung des Konditionensystems (siehe Kapitel 2). In der Vorgehensweise wurden nur absatzmarktbezogene Ober- und Untergrenzen berücksichtigt. Es kann aber noch weitere Engpässe geben, was im nächsten Abschnitt behandelt werden soll.

1.3 Optimale Preise bei Engpässen

Kaum ein Unternehmen bleibt von Engpässen verschont. Sie können an fast jeder Stelle auftauchen. Ende 2021 wird intensiv über Rohmaterialknappheit diskutiert. Wenn Unternehmen z. B. nicht genug Halbleiter-Chips beschaffen können, müssen die beschaffbaren Mengen optimal zugeteilt werden. Zur weiteren Verdeutlichung der Problematik der Engpässe sei ein aktuelles Beispiel aus der Autoindustrie betrachtet:

Für Neuwagen gilt ein Grenzwert von 95 g CO2 pro km [1]. Insofern müssen sich die Unternehmen genau überlegen, welche Fahrzeuge sie noch verkaufen wollen. In einem früheren Beitrag (Produktpolitik bei begrenztem CO2-Ausstoß) hat der Autor gezeigt, wie mit Hilfe relativer Deckungsspannen dieses Optimierungsproblem gelöst werden kann.

Als Ergebnis zeigt sich, dass die Anzahl der Fahrzeuge mit Verbrennungsmotor (Benzin, Diesel, Gas) reduziert werden muss. Die Reduktion sollte mit Fahrzeugen mit geringer Marge beginnen. Durch den Verkauf von E-Fahrzeugen und Plug-in Hybriden können sich die Hersteller - unverständlicherweise - einen CO2-Vorrat aufbauen, den sie dann für die profitablen (und dreckigen) Verbrenner einsetzen können. Für die E-Autos erhält jeder Hersteller im Jahr 2021 CO2-Gutschriften im Wert von ca. 15 T€ pro Fahrzeug (vgl. im Detail Hoberg (2021), S. 1 ff.). Die teuren Fahrzeuge mit hoher relativer Deckungsspanne werden als erstes in den Verkauf geschickt. Die relative Deckungsspanne ist in diesem Fall wie folgt definiert:

drel	Relative Deckungsspanne, in €/FE (Faktoreinheit)
d	Absolute Deckungsspanne in €/ME
PK	Produktionskoeffizient, in FE/ME

Der Produktionskoeffizient PK wird in diesem Fall gemessen in g CO2 oberhalb der Grenze von 95 g. Ein Fahrzeug mit 115 g CO2 pro km hat somit einen PK von 20 g CO2 pro km.

Die Hersteller müssen - wie auch die Zulassungszahlen zeigen - für Fahrzeuge mit geringer relativer Deckungsspanne eine Vollbremsung hinlegen. Dies wird über eine kräftige Erhöhung der Nettopreise bewerkstelligt, wobei die Listenpreise aber kaum steigen. Dass dies in der Praxis so funktioniert, zeigt das Managermagazin vom 29.10.2021. Demnach hat Daimler trotz weniger Verkäufe den Umsatz fast gehalten und den Gewinn sogar gesteigert. Dazu trug sicher auch bei, dass die knappen Halbleiterchips zunächst für solche Fahrzeuge eingesetzt wurden und werden, welche eine hohe Marge aufweisen. Dies sind die S-Klasse und die E-Fahrzeuge.

Daher haben viele Autobauer ihre Rabattaktionen und Verkaufsförderungsmaßnahmen für kleine wenig profitable Fahrzeuge (im Sinne von geringer relativer Deckungsspanne) zurückgefahren. Eine noch schlimmere Folge besteht darin, dass Kleinwagen von den meisten Herstellern nicht mehr weiterentwickelt wird, obwohl sie den geringsten Ressourcenverbrauch aufweisen und bei richtiger Rechnung auch deutlich weniger CO2 ausstoßen, solange nicht aller Strom erneuerbar ist. Da offizielle Preiserhöhungen nur schwer akzeptiert werden, müssen andere Maßnahmen ergriffen werden, um die Kunden vom Kauf günstiger Produkte abzuhalten.

2. Rückwärtsrechnung der Preise

Nachdem im vorigen Abschnitt der optimale Nettopreis bestimmt wurde, kann im nächsten Schritt das Konditionensystem aufgebaut werden, welches die Brücke vom Listenpreis bis zum optimalen Nettopreis schlägt. In der Einleitung ist bereits erwähnt worden, dass häufig eine Vielzahl von Konditionen berücksichtigt werden müssen, bis der tatsächliche Nettopreis korrekt ermittelt ist. Es ist immer wieder festzustellen, dass Unternehmen die Höhe der Abzüge unterschätzen. Wenn wirklich alle Abzüge berücksichtigt werden, bleibt als Nettopreis fast immer deutlich weniger übrig als erwartet.

Die Aufgabenstellung liegt nun darin herauszufinden, wie bei gleichem Listenpreis die Konditionen / Rabatte gesetzt werden müssen, damit der optimale Nettopreis resultiert. (Allerdings kann es sein, dass die Kunden auf einer früheren Ebene ihre Entscheidung treffen, also z. B. die Wirkung der Zahlungsziele nicht oder stärker gewichten). In der folgenden Abb. 1 ist für den Fall 1 eine übliche Kalkulation aufgeführt, welche die wichtigsten Elemente (aber sicher nicht alle) enthält:



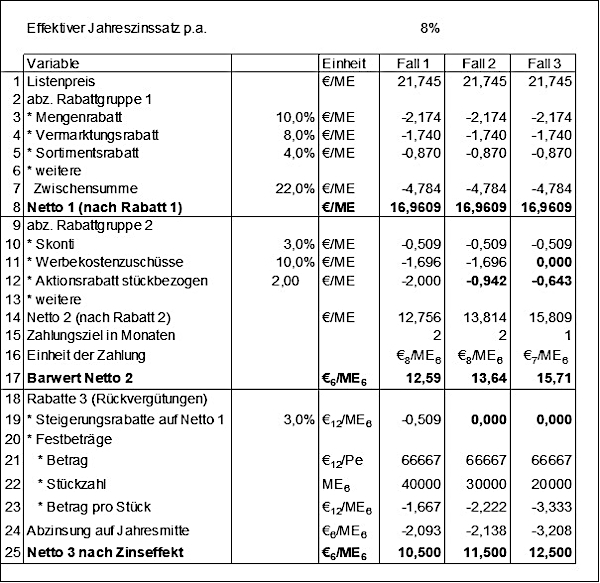Abb.1: Konditionensystem: Vom Listenpreis zum Nettopreis nach Zinsen

Da die Kalkulationen über mehrere Stufen laufen, können geringe Rundungsdifferenzen auftauchen. Im Basisfall ist in Zeile 1 ein Listenpreis von 21,745 €/ME angenommen, der dann auch für die anderen Fälle gilt. Im ersten Schritt sind nun die Rabatte der Gruppe 1 abzuziehen, von denen einige beispielhaft aufgeführt sind. Üblicherweise werden sie in Prozent vom Listenpreis, der kundenspezifisch sein kann, ausgedrückt. Es ergibt sich in Zeile 8 der Netto 1 (Preis), der dann auch auf der Rechnung erscheint, so dass man ihn in der Praxis auch Rechnungspreis nennt. Ab Zeile 10 finden sich die Abzüge der Rabattgruppe 2, die teilweise auch stückbezogen gewährt werden, was insb. für den Fall gilt, dass der Hersteller eine Sonderaktion mit günstigen Preisen unterstützen möchte.

Wenn der Hersteller nun den Nettopreis steigern möchte, wird er Rabatte reduzieren. Im Beispiel ist angenommen, dass im Fall 3 keine Werbekostenzuschüsse mehr bezahlt werden (Zeile 11). Und auch die Aktionsrabatte werden für Fall 2 und 3 reduziert (Zeile 12, Werte gerundet). Als Konsequenz muss akzeptiert werden, dass die abgesetzte Menge deutlich schrumpft (siehe Zeile 22). Eine später folgende Analyse wird zeigen, dass der Deckungsbeitragsverlust sich in Grenzen hält, weil ja höhere Preise durchgesetzt werden.

Der Nettopreis 2, also nach Abzug aller Rabatte der Gruppe 2, wird in Zeile 14 ausgewiesen. Da für ihn 2 Monate Zahlungsziel gelten, weist er die Einheit €8 / ME6 auf. Dies bedeutet, dass die Lieferung im Durchschnitt zur Jahresmitte (t=6) anfällt (Index t gibt das jeweilige Monatsende an), und dass die Zahlung durchschnittlich erst nach 8 Monaten (t=8) erfolgt.

Zur besseren Vergleichbarkeit müssen die Einzahlungen auf einen einheitlichen Vergleichszeitpunkt bezogen werden. Für Deckungsbeitragskalkulationen bietet sich die Jahresmitte an (also t=6 für Ende Juni), weil dort auch die durchschnittliche Lieferung stattfindet. Durch die Abzinsung um 2 Monate (bzw. 1 Monat in Fall 3) werden die eigentlich erst später anfallenden Zahlungen auf die Jahresmitte bezogen. In Zeile 17 finden sich dann die auf die Jahresmitte bezogenen Preise. Die Einheit beträgt dann €6 / ME6 (vgl. zu dieser genaueren Schreibweise Hoberg (2018a), S. 468 ff.).

In der dritten Rabattgruppe finden sich die Rückvergütungen, die üblicherweise am Jahresende fällig werden. Diese können stückbezogen, prozentual oder als Festbetrag gewährt werden. Für die Fälle 2 und 3 ist angenommen, dass keine Steigerungsrabatte mehr gegeben werden, weil das Unternehmen bereit ist, auf Stückzahlen zu verzichten, da Engpässe vorliegen.

Festbeträge sind nicht gut, wenn die Mengen sinken, weil sie sich dann schlechter auf die Produkte verteilen. Dieser Effekt ist in den Zeilen 21 bis 23 abgebildet. Da diese Zahlungen häufig erst am Jahresende anfallen, müssen sie auf die Jahresmitte abgezinst werden, was in Zeile 24 geschieht. In der letzten Zeile erhält man dann den Nettopreis. Für den ersten Fall beträgt er 10,5 €6 / ME6 wie im obigen Beispiel der Preisabsatzfunktion. Wenn jetzt die Menge reduziert werden muss, weil Knappheit bei Inputfaktoren vorliegen, empfiehlt sich eine Verschlechterung der Konditionen, die allerdings von Mengenverlusten begleitet wird. Dies geht aus den Fällen 2 und 3 hervor. Die Verschlechterungen führen zu höheren Netto 3 Preisen von 11,50 und 12,50 statt 10,50 €6 / ME6. Es liegt somit eine Abweichung zum deckungsbeitragsoptimalen Preis vor. Die Wirkung auf den Gewinn wird im nächsten Abschnitt analysiert.

Ermittlung des Deckungsbeitragsverlustes

Die Erhöhungen des Nettopreises waren die Antwort auf die Notwendigkeit, die Stückzahlen zu reduzieren, wenn nicht genügend Inputfaktoren zur Verfügung stehen. Zu den Inputfaktoren können neben Rohstoffen, Halbfertigfabrikate wie Halbleiterchips usw. auch Verschmutzungsrechte wie das CO2 bei E-Autos zählen. Solche Engpässe führen zu Gewinnreduktionen, die nun quantifiziert werden sollen. In Abb. 2 findet sich in Zeile 1 der variable Stückkostensatz, welcher angibt, wie sich die Kosten in Abhängigkeit der Mengen ändern. Wichtig ist bei der Bestimmung wieder ein Nachdenken über den zeitlichen Anfall der zusätzlichen Kosten. Wenn die Umsätze auf die Jahresmitte (Ende des Monats 6) bezogen sind, muss das auch für die Kosten gelten, weil ansonsten nicht saldiert werden darf. Da die Auszahlungen für die Produktion häufig vor der Verladung anfallen, müssen die Kosten häufig auf t=6 aufgezinst werden.

Im Weiteren werden die Nettopreise 3 nach Berücksichtigung der Zinseffekte und die jeweils resultierenden Mengen aus Abb. 1 übernommen. Die Mengenänderungen in Zeile 4 der Abb. 2 sind beträchtlich. In Fall 2 reduzieren sie sich um 25 bzw. 50 %. Auch die Nettoumsätze werden geringer, aber nur noch um 17,9 und 40,5 % wie die Zeile 6 zeigt, weil die erhöhten Preise einen Teil der Wirkung des Mengeneffektes auffangen.



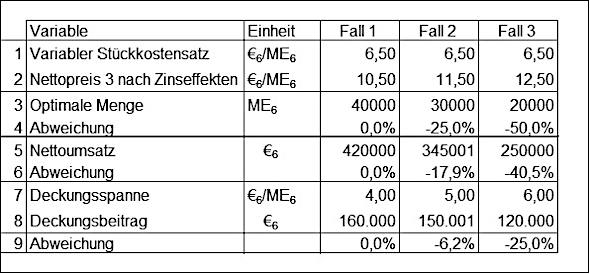Abb. 2: Auswirkungen höherer Preise auf Menge, Umsatz und Deckungsbeitrag

Ausgeglichen werden die Umsatzverluste teilweise durch höhere Deckungsspannen, so dass die Deckungsbeiträge in Zeile 8 nur noch um 6,2 % bzw. 25 % fallen. Die Analyse wurde nur für ein einziges Produkt oder eine einzige Produktgruppe durchgeführt, für die eine Mengenreduktion aus übergeordneten Gründen sinnvoll war. Wenn jetzt noch Mixeffekte aus dem gesamten Produktspektrum genutzt werden können, kann das Bild noch viel besser aussehen. Gute Produkte werden bei ähnlicher Menge noch besser, und margenschwache Produkte werden überproportional gebremst, indem die Nachlässe insb. in Gruppe 2 und 3 zusammengestrichen werden.

Wie gut so eine kombinierte Strategie funktionieren kann, zeigt eine Pressemitteilung von BMW (SZ 3.11.2021): Man habe eine "bessere Preisdurchsetzung" geschafft. Im Klartext: Es wurden weniger Rabatte gegeben, Vertriebsförderungen waren kaum nötig und es wurde ein höherwertiger Mix erreicht. Und das alles ohne offizielle Preiserhöhungen. Auf diese Weise konnte das Ergebnis gesteigert werden, obwohl durch den Engpass von Halbleiterchips die Anzahl der verkauften Fahrzeuge gesunken war.

3. Schlussfolgerungen

Aus verschiedenen Gründen können sich Unternehmen gezwungen sehen, ihre Absatzmengen zu reduzieren:

• Engpässe bei Rohstoffen und Halbfertigfabrikaten
• Anstieg der Energiepreise
• Personalmangel
• Restriktionen durch Umweltvorschriften
• Niedriges Preisniveau u. ä.

Wenn bekannt ist, dass die Mengen zurückgefahren werden müssen, muss das Controlling sorgfältig bestimmen, wie das geschehen soll. Durch Mengenreduktionen entstehen allerdings im ersten Schritt negative Effekte auf die Nettoumsätze und die Deckungsbeiträge. Diese können allerdings gemildert werden, wenn die Preise als Mittel zur Mengenreduktion erhöht werden. Es empfiehlt sich, die Erhöhungen nicht offensichtlich zu machen, sondern über verringerte Rabatte und Verkaufsförderungsprogramme. Der Preiseffekt kann einen Teil des negativen Mengeneffektes auffangen. In umfangreichen Produktportfolios kann es sogar zu einer Steigerung der Deckungsbeiträge kommen, wenn Produkte mit hoher relativer Deckungsspanne gefördert werden, während schwache Produkte durch kräftige Erhöhungen im Nettopreis gebremst werden.

Wie auch die Praxis beispielsweise bei Kleinwagen zeigt, können selbst zweistellige Preiserhöhungen oft dadurch durchgesetzt werden, dass die Konditionen verschlechtert werden. Dann ist eine offene Preiserhöhung gar nicht notwendig. Zudem kann ein Umsteuern im Sortimentsmix eine ähnliche Erhöhung der durchschnittlichen Deckungsbeiträge bewirken. Der Controller ist mehr denn je gefordert. Umgekehrt können Preissenkungen offen beworben werden, wenn dadurch die Marke nicht bestätigt wird.


Fußnote

[1] Aus Gründen der besseren Lesbarkeit wird hier die umgangssprachliche Darstellung CO2 verwendet und nicht die wissenschaftlich korrekte Darstellung CO₂.

letzte Änderung P.D.P.H. am 07.11.2022 Autor:  Dr. Peter Hoberg Bild:  panthermedia.net / violetkaipa

Autor:in

	Herr Prof. Dr. Peter Hoberg Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung.
weitere Fachbeiträge des Autors | Forenbeiträge