INDUS Holding AG
Bergisch Gladbach bei Köln
| Nettopreisszenario |
Nettopreis in €/ME |
Var. Stückk. in €/ME |
Deckungssp. in €/ME |
Menge in ME/Pe |
DB in €/Pe |
DB-Marge in €DB/€NU |
| 1 | 100,00 | 20,00 | 80,00 | 1000 | 80.000 | 80,00 % |
| 2 | 90,00 | 20,00 | 70,00 | 1000 | 70.000 | 77,78 % |
| 3 | 80,00 | 20,00 | 60,00 | 1000 | 60.000 | 75,00 % |
| 4 | 70,00 | 20,00 | 50,00 | 1000 | 50.000 | 71,43 % |
| 5 | 60,00 | 20,00 | 40,00 | 1000 | 40.000 | 66,67 % |
| 6 | 50,00 | 20,00 | 30,00 | 1000 | 30.000 | 60,00 % |
| 7 | 40,00 | 20,00 | 20,00 | 1000 | 20.000 | 50,00 % |
| 8 | 30,00 | 20,00 | 10,00 | 1000 | 10.000 | 33,33 % |
| 9 | 20,00 | 20,00 | 0,00 | 1000 | 0 | 0,00 % |
| 10 | 10,00 | 20,00 | -10,00 | 1000 | -10.000 | -100,00 % |
| Nettopreis-szenario | Preisänderung |
Neuer Preis in €/ME |
Neue DSp in €/ME |
Neue Db-Marge in €DB/€NU |
Änderung Menge |
Neue Menge in ME/Pe |
Neuer Db in €/Pe |
| 1 | 1,00 % | 101,00 | 81,00 | 80,20 % | -1,23 % | 987,65 | 80.000 |
| 2 | 1,00 % | 90,90 | 70,90 | 78,00 % | -1,27 % | 987,31 | 70.000 |
| 3 | 1,00 % | 80,80 | 60,80 | 75,25 % | -1,32 % | 986,84 | 60.000 |
| 4 | 1,00 % | 70,70 | 50,70 | 71,71 % | -1,38 % | 986,19 | 50.000 |
| 5 | 1,00 % | 60,60 | 40,60 | 67,00 % | -1,48 % | 985,22 | 40.000 |
| 6 | 1,00 % | 50,50 | 30,50 | 60,40 % | -1,64 % | 983,61 | 30.000 |
| 7 | 1,00 % | 40,40 | 20,40 | 50,50 % | -1,96 % | 980,39 | 20.000 |
| 8 | 1,00 % | 30,30 | 10,30 | 33,99 % | -2,91 % | 970,87 | 10.000 |
| 9 | 1,00 % | 20,20 | 0,20 | 0,99 % | -100,00 % | 0,00 | 0 |
| 10 | 1,00 % | 10,10 | -9,90 | -98,02 % | 1,01 % | 1010,10 | -10.000 |
| Nettopreis-szenario | Preisänderung |
Neuer Preis in €/ME |
Neue DSp in €/ME |
Neue Db-Marge in €DB/€NU |
Änderung Menge |
Neue Menge in ME/Pe |
Neuer Db in €/Pe |
| 1 | 1,00 % | 101,00 | 81,00 | 80,20 % | -1,23 % | 987,65 | 80.000 |
| 2 | 5,00 % | 105,00 | 85,00 | 80,95 % | -5,88 % | 941,18 | 80.000 |
| 3 | 10,00 % | 110,00 | 90,00 | 81,82 % | -11,11 % | 888,89 | 80.000 |
| 4 | 20,00 % | 120,00 | 100,00 | 83,33 % | -20,00 % | 800,00 | 80.000 |
| 5 | 30,00 % | 130,00 | 110,00 | 84,62 % | -27,27 % | 727,27 | 80.000 |
| 6 | 40,00 % | 140,00 | 120,00 | 85,71 % | -33,33 % | 666,67 | 80.000 |
| 7 | 50,00 % | 150,00 | 130,00 | 86,67 % | -38,46 % | 615,38 | 80.000 |
| 8 | 60,00 % | 160,00 | 140,00 | 87,50 % | -42,86 % | 571,43 | 80.000 |
| 9 | 80,00 % | 180,00 | 160,00 | 88,89 % | -50,00 % | 500,00 | 80.000 |
| 10 | 100,00 % | 200,00 | 180,00 | 90,00 % | -55,56 % | 444,44 | 80.000 |
DB = d * x = (pN – kv) *in € in der betrachteten Periode (Pe)
| DB | Deckungsbeitrag, in €/Pe |
| D | Deckungsspanne in €/ME |
| x | Absatzmenge in ME/Pe |
| pN | Nettopreis (nach allen Rabatten und Zahlungszielen) in €/ME |
| kV | Variable Stückkosten in €/ME |
DBneu = (pN * (1 + ∆p) – kv) * x * (1 + ∆x)in € in der betrachteten Periode
∆p Preisänderung ∆x Mengenänderung
(pN - kV) = (pN * (1 + ∆p) - kv) * (1 + ∆x)Die kritische Mengenänderung lässt sich also einfach berechnen, wenn man die geplante Preisänderung sowie die relative Deckungsbeitragsmarge d/pN kennt. Wenn 20 % Preiserhöhung geplant sind und die Ursprungsmarge wie in Zeile 1 von Abb. 1 einen Wert von 80% annimmt, erhält man:
∆x = (pN - kv) / (pN * (1 + ∆p) - kv) - 1
= (pN - kv - pN - pN * ∆p + kv) / (pN * (1 + ∆p) - kv)
= - ∆p / ((1 + ∆p) - kv / pN)
= - ∆p / (∆p + d/pN)
∆x = -0,2 / (0,2 + 0,8) = -0,2 = -20%Genau dieses Ergebnis findet sich in Abb. 3.
|
letzte Änderung P.D.P.H. am 02.07.2025 Autor: Dr. Peter Hoberg Bild: panthermedia.net / Dudko |
 |
Herr Prof. Dr. Peter Hoberg
Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung. |
| weitere Fachbeiträge des Autors | Forenbeiträge | |
Nur registrierte Benutzer können Kommentare posten!








 Das Max-Planck-Institut für Biochemie (MPIB) in Martinsried bei München zählt zu den führenden internationalen Forschungseinrichtungen auf den Gebieten der Biochemie, Zell- und Strukturbiologie sowie der biomedizinischen Forschung und ist mit rund 28 wissenschaftlichen Abteilungen und For... Mehr Infos >>
Das Max-Planck-Institut für Biochemie (MPIB) in Martinsried bei München zählt zu den führenden internationalen Forschungseinrichtungen auf den Gebieten der Biochemie, Zell- und Strukturbiologie sowie der biomedizinischen Forschung und ist mit rund 28 wissenschaftlichen Abteilungen und For... Mehr Infos >>
 Börsennotierte Führungsgesellschaft einer mittelständisch geprägten Unternehmensgruppe mit aktuell 46 unmittelbaren Beteiligungen in den Segmenten Engineering, Infrastructure und Material Solutions, Nachhaltige Beteiligungsstrategie "Kaufen, Halten und Entwickeln", Sitz in Bergisch Glad... Mehr Infos >>
Börsennotierte Führungsgesellschaft einer mittelständisch geprägten Unternehmensgruppe mit aktuell 46 unmittelbaren Beteiligungen in den Segmenten Engineering, Infrastructure und Material Solutions, Nachhaltige Beteiligungsstrategie "Kaufen, Halten und Entwickeln", Sitz in Bergisch Glad... Mehr Infos >>
 NIEHOFF ist ein erfolgreiches deutsches, mittelständisches Unternehmen mit internationalen Strukturen und Tradition im Bereich des Sondermaschinenbaus. Mit eigenen Tochtergesellschaften und Niederlassungen in den USA, Brasilien, China, Indien, Tschechien, Schweden, Singapur, Japan, Spanien... Mehr Infos >>
NIEHOFF ist ein erfolgreiches deutsches, mittelständisches Unternehmen mit internationalen Strukturen und Tradition im Bereich des Sondermaschinenbaus. Mit eigenen Tochtergesellschaften und Niederlassungen in den USA, Brasilien, China, Indien, Tschechien, Schweden, Singapur, Japan, Spanien... Mehr Infos >>
 Werde als zertifierter Bilanzbuchhalter/in (m/w/d) ein essenzieller Teil unseres Finanzteams und nutze SAP S/4HANA, um unsere Geschäftsvorgänge digital, zeitgerecht und transparent abzubilden. Mit Deiner tiefgehenden Erfahrung optimierst Du, gemeinsam mit uns, unsere Abläufe und hilfst un... Mehr Infos >>
Werde als zertifierter Bilanzbuchhalter/in (m/w/d) ein essenzieller Teil unseres Finanzteams und nutze SAP S/4HANA, um unsere Geschäftsvorgänge digital, zeitgerecht und transparent abzubilden. Mit Deiner tiefgehenden Erfahrung optimierst Du, gemeinsam mit uns, unsere Abläufe und hilfst un... Mehr Infos >>
 In der ALTANA Gruppe arbeiten Sie in einer einzigartigen Innovationskultur, in der die Förderung individueller Ideen und Fähigkeiten und ein offenes, vertrauensvolles Miteinander großgeschrieben werden. BYK-Gardner bietet Ihnen eine Menge Vorteile. Im Detail: eine angenehme Betriebsgröße, in der ... Mehr Infos >>
In der ALTANA Gruppe arbeiten Sie in einer einzigartigen Innovationskultur, in der die Förderung individueller Ideen und Fähigkeiten und ein offenes, vertrauensvolles Miteinander großgeschrieben werden. BYK-Gardner bietet Ihnen eine Menge Vorteile. Im Detail: eine angenehme Betriebsgröße, in der ... Mehr Infos >>
 Die Bundesanstalt für Immobilienaufgaben (BImA) ist das Immobilienunternehmen des Bundes, das die immobilienpolitischen Ziele der Bundesregierung unterstützt und für fast alle Bundesbehörden die notwendigen Flächen und Gebäude zur Verfügung stellt. Dementsprechend sind wir in ganz Deutsch... Mehr Infos >>
Die Bundesanstalt für Immobilienaufgaben (BImA) ist das Immobilienunternehmen des Bundes, das die immobilienpolitischen Ziele der Bundesregierung unterstützt und für fast alle Bundesbehörden die notwendigen Flächen und Gebäude zur Verfügung stellt. Dementsprechend sind wir in ganz Deutsch... Mehr Infos >>
 Die Bundesanstalt für Immobilienaufgaben (BImA) ist das Immobilienunternehmen des Bundes, das die immobilienpolitischen Ziele der Bundesregierung unterstützt und für fast alle Bundesbehörden die notwendigen Flächen und Gebäude zur Verfügung stellt. Dementsprechend sind wir in ganz Deutsch... Mehr Infos >>
Die Bundesanstalt für Immobilienaufgaben (BImA) ist das Immobilienunternehmen des Bundes, das die immobilienpolitischen Ziele der Bundesregierung unterstützt und für fast alle Bundesbehörden die notwendigen Flächen und Gebäude zur Verfügung stellt. Dementsprechend sind wir in ganz Deutsch... Mehr Infos >>
 Bist Du mit an Bord, wenn es um Nachhaltigkeit und das Erreichen der Klimaziele geht? Dann leiste jetzt bei Techem Deinen aktiven Beitrag dazu, wertvolle Ressourcen zu schonen. Wir sorgen gemeinsam für die digitale Energiewende in Gebäuden. Als ein führender Servicepartner für smarte und nachhalt... Mehr Infos >>
Bist Du mit an Bord, wenn es um Nachhaltigkeit und das Erreichen der Klimaziele geht? Dann leiste jetzt bei Techem Deinen aktiven Beitrag dazu, wertvolle Ressourcen zu schonen. Wir sorgen gemeinsam für die digitale Energiewende in Gebäuden. Als ein führender Servicepartner für smarte und nachhalt... Mehr Infos >>


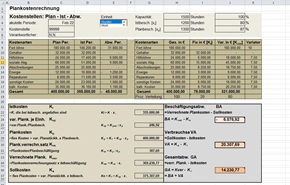





 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>