![Das optimale Produktionsprogramm - Planung mit Engpass und ohne]()
Im Bereich der
Produktions- und
Absatzplanung kann die
Vollkostenrechnung ebenfalls zu falschen
Entscheidungen führen, weil eine
verursachungsgerechte Zurechnung der
Fixkosten auf die einzelnen
Kostenträger nicht möglich ist. Entscheidungen über das gewinnmaximale Produktionsprogramm und Aussagen über die hieraus resultierende
Erfolgsänderung können nur auf der Basis der
Deckungsbeiträge getroffen werden.
Zur Erleichterung des Verständnisses der zugrunde liegenden
Zusammenhänge wird im folgenden Beispiel zunächst von unrealistischen Voraussetzungen ausgegangen. Das Beispiel wird dann durch den schrittweisen Abbau der Voraussetzungen in realistische Verhältnisse überführt.
1. Produktionsprogramm - Planung ohne Engpass
Es gelten zunächst die folgenden
Voraussetzungen:
- Es liegen keine Beschränkungen der Absatzmengen vor, was produziert wird kann auch verkauft werden.
-
Alle hergestellten Produkte belasten die Produktionsanlagen gleichmäßig (d.h. die Maschinenbearbeitungszeiten sind bei allen Produkten gleich). Es wird zunächst unterstellt, dass jedes der hergestellten Produkte die Fertigungsanlagen 30 Minuten beansprucht.
-
Die vorhandenen Kapazitäten betragen 300 Maschinenstunden und sind voll ausgelastet.
Ein Betrieb stellt
vier Produkte her, deren Maschinenbearbeitungszeit jeweils 30 Minuten beträgt. Es stehen insgesamt 300 Maschinenstunden zur Verfügung. Von jedem der vier Produkte können also maximal 600 Einheiten produziert werden. Die Produkte können auch in jeder beliebigen Kombination hergestellt werden (z. B. A = 250, B = 200; C = 50 und D = 100).
Anzeige

Mit der
Excel-Vorlage „Rollierende Liquiditätsplanung auf Wochenbasis“ erstellen Sie schnell ein Bild ihrer operativen
Liquiditätslage für die nächsten (bis zu 52) Wochen. Die Datei erlaubt nicht nur die Eingabe aller voraussichtlichen Zahlungsein- und -ausgänge (Plan-Daten), sondern berücksichtigt auch die Anfangs- und Schlussbestände auf den Konten (IST-Daten).
Preis 59,50 EUR ....
Download hier >>
Das aktuelle
Produktionsprogramm des Betriebes sieht folgendermaßen aus, wobei Preise und Stückkosten der vier Produkte bekannt sind.
|
Produkt
|
Preis
|
Stückkosten
|
Absatz
|
|
A
|
6
|
4
|
200
|
|
B
|
9
|
3
|
50
|
|
C
|
4
|
3
|
250
|
|
D
|
10
|
7
|
100
|
|
Summe:
|
|
|
600
|
Zu ermitteln ist zunächst das
Betriebsergebnis aufgrund der aktuellen Daten:
|
Produkt
|
Preis
|
Stückkosten
|
Absatz
|
Erlöse
|
Kosten
|
Gewinn
|
|
A
|
6
|
4
|
200
|
1.200
|
800
|
400
|
|
B
|
9
|
3
|
50
|
450
|
150
|
300
|
|
C
|
4
|
3
|
250
|
1.000
|
750
|
250
|
|
D
|
10
|
7
|
100
|
1.000
|
700
|
300
|
|
Summe:
|
|
|
600
|
3.650
|
2.400
|
1.250
|
Der
Gewinn beim aktuellen Produktionsprogramm beträgt 1.250 €. Ein Kostenrechner soll feststellen, ob sich das Betriebsergebnis durch ein
alternatives Produktionsprogramm verbessern lässt. Aufgrund der Vollkostenrechnung fällt die Entscheidung für das Produkt mit dem höchsten Stückgewinn:
|
Produkt
|
Preis
|
Stückkosten
|
Stückgewinn
|
Absatz
|
Erlöse
|
Kosten
|
Gewinn
|
|
A
|
6
|
4
|
2
|
0
|
0
|
0
|
0
|
|
B
|
9
|
3
|
6
|
600
|
5.400
|
1.800
|
3.600
|
|
C
|
4
|
3
|
1
|
0
|
0
|
0
|
0
|
|
D
|
10
|
7
|
3
|
0
|
0
|
0
|
0
|
|
Summe:
|
|
|
|
|
5.400
|
1.800
|
3.600
|
Das
Betriebsergebnis verbessert sich von 1.250 € auf 3.600 €. Es scheint so, als sei es dem Kostenrechner tatsächlich gelungen, durch Veränderung des Produktionsprogramms das Betriebsergebnis zu verbessern. Das neue BE ist aus folgendem Grunde jedoch falsch bestimmt:
Die in dem Betrieb vorhandenen, aber dem Vollkostenrechner nicht bekannten
Fixkosten sind beim ursprünglichen Produktionsprogramm auf vier Produkte verteilt. Wird die Produktion nun nur auf ein Produkt umgestellt, muss dieses eine Produkt auch diejenigen Fixkosten tragen, die vorher den übrigen drei Produkten zugerechnet waren. Dadurch ergeben sich für das ausgewählte Produkt
neue Stückkosten, der Stückgewinn und die Höhe der Kosten ändern sich.
Fazit: Eine sinnvolle Entscheidung über das gewinnmaximale Produktionsprogramm aufgrund der Vollkostenrechnung ist nicht möglich. Die Entscheidung muss mit Hilfe der Deckungsbeitragsrechnung getroffen werden, die Höhe der fixen und variablen Kosten muss bekannt sein. Für die Aufteilung der gesamten Stückkosten in fixe und variable Teile werden die folgenden Werte unterstellt:
|
Produkt
|
Preis
|
kv
|
kf
|
db
|
Absatz
|
kf
|
DB
|
Gewinn
|
|
A
|
6
|
1
|
3
|
5
|
200
|
600
|
1000
|
400
|
|
B
|
9
|
2
|
1
|
7
|
50
|
50
|
350
|
300
|
|
C
|
4
|
1
|
2
|
3
|
250
|
500
|
750
|
250
|
|
D
|
10
|
2
|
5
|
8
|
100
|
500
|
800
|
300
|
|
Summe:
|
|
|
|
|
600
|
1.650
|
2.900
|
1.250
|
Die Werte der Spalten errechnen sich wie folgt:
- db = p - kv
- Kf = kf * Absatz
- DB = db * Absatz
- Gewinn = DB - Kf
Die
Gewinnermittlung beim alten Produktionsprogramm aufgrund der Vollkosten- und der
Teilkostenrechnung führen selbstverständlich zum gleichen Ergebnis. Als Entscheidungskriterium für die Zusammenstellung des optimalen Produktionsprogramms aufgrund der Teilkostenrechnung werden nun aber die
Stückdeckungsbeiträge herangezogen. Es wird das Produkt mit dem höchsten Stückdeckungsbeitrag hergestellt:
|
Produkt
|
Preis
|
kv
|
kf
|
db
|
Absatz
|
Db
|
Gewinn
|
|
A
|
6
|
1
|
3
|
5
|
0
|
0
|
0
|
|
B
|
9
|
2
|
1
|
7
|
0
|
0
|
0
|
|
C
|
4
|
1
|
2
|
3
|
0
|
0
|
0
|
|
D
|
10
|
2
|
5
|
8
|
600
|
4.800
|
3.150
|
|
Summe:
|
|
|
|
|
600
|
4.800
|
3.150
|
Das Produkt D erzielt einen
Gesamtdeckungsbeitrag von 4.800 €. Da die Fixkosten auch nach Umstellung des Produktionsprogramms in gleicher Höhe (1.650 €) vorhanden sind, ergibt sich ein Gewinn von:
4.800 - 1.650 = 3.150 €.
2. Planung mit Engpass
Bei Vorliegen von
Produktions- bzw.
Absatzengpässen ist die Entscheidung über die Produktpalette nach der Höhe der Stückdeckungsbeiträge zu treffen. Das Produkt mit dem höchsten Stückdeckungsbeitrag ist mit der maximal möglichen Menge herzustellen, dann das Produkt mit dem zweithöchsten Stückdeckungsbeitrag usw.
Die
Voraussetzungen des vorhergehenden Beispiels werden folgendermaßen geändert: Die maximal produzierbare Menge liegt nach wie vor bei 600 Einheiten (18.000 Maschinenminuten). Aufgrund der Situation auf den Absatzmärkten für die vier Produkte ergeben sich folgende Beschränkungen:
Die maximal absetzbaren Mengen sind:
|
Produkt
|
Einheiten
|
|
A
|
100
|
|
B
|
300
|
|
C
|
200
|
|
D
|
250
|
Auf Grund der Stückdeckungsbeiträge ergibt sich folgendes
Produktionsprogramm:
|
Produkt
|
Preis
|
kv
|
kf
|
db
|
Absatz
|
DB
|
|
A
|
6
|
1
|
3
|
5
|
50
|
250
|
|
B
|
9
|
2
|
1
|
7
|
300
|
2.100
|
|
C
|
4
|
1
|
2
|
3
|
0
|
0
|
|
D
|
10
|
2
|
5
|
8
|
250
|
2.000
|
|
Summe:
|
|
|
|
|
600
|
4.350
|
Von den Produkten D und B werden die
absetzbaren Mengen hergestellt, weil diese beiden Produkte die höchsten Stückdeckungsbeiträge erwirtschaften. Den dritthöchsten Stückdeckungsbeitrag hat dann Produkt A, von dem zwar 100 Einheiten abgesetzt werden könnten, die Kapazität reicht jedoch nur noch für die Herstellung von 50 Stück aus. Das Produkt C mit dem niedrigsten Stückdeckungsbeitrag wird nicht hergestellt. Der Gewinn nach der Zusammenstellung des neuen Produktionsprogramms errechnet sich wie folgt:
G = DB - Kf = 4.350 - 1.650 = 2.700
3. Planung mit relativen Deckungsbeiträgen
Die
absoluten Stückdeckungsbeiträge können nur dann zur Planung der Produktpalette herangezogen werden, wenn alle Produkte die Produktionsanlagen gleichmäßig belasten. Sind jedoch zur Bearbeitung der verschiedenen Produkte auch unterschiedliche Maschinenlaufzeiten erforderlich, so dienen die relativen Deckungsbeiträge als Entscheidungskriterium.
Unter einem
relativen Deckungsbeitrag versteht man den Stückdeckungsbeitrag eines Produktes pro Zeiteinheit, also z.B. pro Maschinenminute oder pro Maschinenstunde.
Es stehen pro
Betrachtungsperiode nach wie vor 300 Maschinenstunden (18.000 Minuten) zur Verfügung. Die Produkte benötigen die folgenden Maschinenbearbeitungszeiten in Minuten:
|
Produkt
|
Bearbeitungszeit in Min.
|
|
A
|
25
|
|
B
|
140
|
|
C
|
30
|
|
D
|
20
|
über die Zusammensetzung der Produktpalette wird nun aufgrund der
relativen Deckungsbeiträge (Deckungsbeiträge pro Maschinenminute) entschieden.
|
Produkt
|
db
|
Minuten
|
rel. db
|
Absatz
|
Zeitverbrauch
|
|
A
|
5
|
25
|
0,20
|
100
|
2.500
|
|
B
|
7
|
140
|
0,05
|
32
|
4.500
|
|
C
|
3
|
30
|
0,10
|
200
|
6.000
|
|
D
|
8
|
20
|
0,40
|
250
|
5.000
|
|
Summe:
|
|
|
|
|
18.000
|
Die
Produktrangfolge lautet: D, A, C, B.
Es stehen insgesamt 300 * 60 = 18.000 Maschinenminuten zur Verfügung. Für die Herstellung von D und A werden insgesamt 7.500 Maschinenminuten verbraucht, es verbleiben also noch 10.500 Maschinenminuten. Die Produktion der von Produkt C absetzbaren Menge von 200 Einheiten beansprucht weitere 6.000 Maschinenminuten. Nun verbleiben noch 4.500 Minuten, in denen von Produkt B 32 Stück hergestellt werden können.
4. Ermittlung des Betriebsergebnisses:
|
Produkt
|
db
|
Minuten
|
rel. db
|
Absatz
|
DB
|
|
A
|
5
|
25
|
0,20
|
100
|
500
|
|
B
|
7
|
140
|
0,05
|
32
|
224
|
|
C
|
3
|
30
|
0,10
|
200
|
600
|
|
D
|
8
|
20
|
0,40
|
250
|
2.000
|
|
Summe:
|
|
|
|
|
3.324
|
BE = DB - Kf = 3.324 - 1.650 = 1.674
letzte Änderung E.R.
am 12.04.2023
Autor:
Dipl. Volkswirt Friedrich Schnepf
|
Bleiben Sie auf dem Laufenden mit unserem Newsletter
Tragen Sie sich für den
kostenfreien und unverbindlichen
Newsletter von Controlling-Portal.de ein und erhalten Sie jeden Monat aktuelle Neuigkeiten für Controller. Wir informieren Sie über neue Fachartikel, über wichtige News, aktuelle Stellenangebote, interessante Tagungen und Seminare. Wir empfehlen Ihnen spannende Bücher und geben Ihnen nützliche Excel-Tipps. Verpassen Sie nie mehr wichtige Diskussionen im Forum und stöbern Sie in Software-Angeboten, die Ihnen den Arbeitsalltag erleichtern.
Beispiel-Newsletter >>
Jetzt Newsletter gratis erhalten
Eigenen Fachbeitrag veröffentlichen?
Sie sind Autor einer Fachpublikation oder Entwickler einer Excel-Vorlage? Gern können Sie sich an der Gestaltung der Inhalte unserer Fachportale beteiligen! Wir bieten die Möglichkeit Ihre Fachpublikation (Fachbeitrag, eBook, Diplomarbeit, Checkliste, Studie, Berichtsvorlage ...) bzw. Excel-Vorlage auf unseren Fachportalen zu veröffentlichen bzw. ggf. auch zu vermarkten.
Mehr Infos >>






 Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT.
Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT. Wie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.
Wie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.  Viel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.
Viel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.
 MESSRING ist Branchenführer für Crashtest-Technologie. Seit mehr als fünf Jahrzehnten machen wir mit unseren Produkten und Dienstleistungen Mobilität sicherer – und das weltweit. Unsere Systeme ermöglichen es Unternehmen, Transportmittel zu entwickeln, die Menschen schützen und Leben im Straßenve... Mehr Infos >>
MESSRING ist Branchenführer für Crashtest-Technologie. Seit mehr als fünf Jahrzehnten machen wir mit unseren Produkten und Dienstleistungen Mobilität sicherer – und das weltweit. Unsere Systeme ermöglichen es Unternehmen, Transportmittel zu entwickeln, die Menschen schützen und Leben im Straßenve... Mehr Infos >>
 Wir sind ein zukunftsorientiertes, modernes Entsorgungsunternehmen mit ca. 200 Mitarbeitern. Mit unserer 50-jährigen Erfahrung steht die MEAB als öffentliches Unternehmen der Bundesländer Brandenburg und Berlin für einen verantwortungsvollen Umgang mit Abfällen. Wir erbringen für Akteure aus Indu... Mehr Infos >>
Wir sind ein zukunftsorientiertes, modernes Entsorgungsunternehmen mit ca. 200 Mitarbeitern. Mit unserer 50-jährigen Erfahrung steht die MEAB als öffentliches Unternehmen der Bundesländer Brandenburg und Berlin für einen verantwortungsvollen Umgang mit Abfällen. Wir erbringen für Akteure aus Indu... Mehr Infos >>
 Sie sind ein versierter Zahlenexperte mit Führungstalent und suchen eine Aufgabe, in der Ihr Können wirklich geschätzt wird? Das bieten wir Ihnen: Polstermöbel Fischer zählt mit rund 250 Mitarbeitenden zu den großen Polstermöbel-Filialunternehmen in Deutschland mit dem Ziel die Nr. 1 zu sein! Wir... Mehr Infos >>
Sie sind ein versierter Zahlenexperte mit Führungstalent und suchen eine Aufgabe, in der Ihr Können wirklich geschätzt wird? Das bieten wir Ihnen: Polstermöbel Fischer zählt mit rund 250 Mitarbeitenden zu den großen Polstermöbel-Filialunternehmen in Deutschland mit dem Ziel die Nr. 1 zu sein! Wir... Mehr Infos >>
 Die Fraunhofer-Gesellschaft (www.fraunhofer.de) betreibt in Deutschland derzeit 76 Institute und Forschungseinrichtungen und ist eine der führenden Organisationen für anwendungsorientierte Forschung. Rund 32 000 Mitarbeitende erarbeiten das jährliche Forschungsvolumen von 3,4 Milliarden ... Mehr Infos >>
Die Fraunhofer-Gesellschaft (www.fraunhofer.de) betreibt in Deutschland derzeit 76 Institute und Forschungseinrichtungen und ist eine der führenden Organisationen für anwendungsorientierte Forschung. Rund 32 000 Mitarbeitende erarbeiten das jährliche Forschungsvolumen von 3,4 Milliarden ... Mehr Infos >>
 Techtronic Industries ist weltweit führend in der Herstellung und im Vertrieb von hochwertigen Elektrowerkzeugen für den DIY-Markt und den Profieinsatz sowie von Gartengeräten. Ein strategischer Fokus auf leistungsstarke Marken, innovative Produkte und außergewöhnliche Menschen bestimmt unseren E... Mehr Infos >>
Techtronic Industries ist weltweit führend in der Herstellung und im Vertrieb von hochwertigen Elektrowerkzeugen für den DIY-Markt und den Profieinsatz sowie von Gartengeräten. Ein strategischer Fokus auf leistungsstarke Marken, innovative Produkte und außergewöhnliche Menschen bestimmt unseren E... Mehr Infos >>
 LITEF-Produkte sind weltweit in einer Vielzahl von Anwendungen im Einsatz. Unsere Lösungen und Erfahrungen bieten wir Kunden, die dynamische Vorgänge (Beschleunigungen und Drehungen) messen und regeln wollen, Lage und Kurs von Fahrzeugen ermitteln oder navigieren wollen – auf dem Land, in... Mehr Infos >>
LITEF-Produkte sind weltweit in einer Vielzahl von Anwendungen im Einsatz. Unsere Lösungen und Erfahrungen bieten wir Kunden, die dynamische Vorgänge (Beschleunigungen und Drehungen) messen und regeln wollen, Lage und Kurs von Fahrzeugen ermitteln oder navigieren wollen – auf dem Land, in... Mehr Infos >>
 Du hast Lust in einer Mannschaft zu arbeiten, für die partnerschaftliches Miteinander an erster Stelle steht? Mit Menschen, die genauso viel Freude an ihrer Arbeit haben wie du? Dann komm zu uns. Die Paul Bauder GmbH & Co. KG in Stuttgart ist seit über 160 Jahren inhabergeführt und Europas führen... Mehr Infos >>
Du hast Lust in einer Mannschaft zu arbeiten, für die partnerschaftliches Miteinander an erster Stelle steht? Mit Menschen, die genauso viel Freude an ihrer Arbeit haben wie du? Dann komm zu uns. Die Paul Bauder GmbH & Co. KG in Stuttgart ist seit über 160 Jahren inhabergeführt und Europas führen... Mehr Infos >>
 Unsere ausgeprägte Leidenschaft für Live Entertainment, Musicals und Theateraufführungen auf höchstem Niveau ist, was uns bei Stage verbindet. Diese gemeinsame Begeisterung macht aus den vielfältigsten Mitarbeitenden in unterschiedlichsten Jobs ein hingebungsvolles Team: ein echtes „Wir“. Und das... Mehr Infos >>
Unsere ausgeprägte Leidenschaft für Live Entertainment, Musicals und Theateraufführungen auf höchstem Niveau ist, was uns bei Stage verbindet. Diese gemeinsame Begeisterung macht aus den vielfältigsten Mitarbeitenden in unterschiedlichsten Jobs ein hingebungsvolles Team: ein echtes „Wir“. Und das... Mehr Infos >>


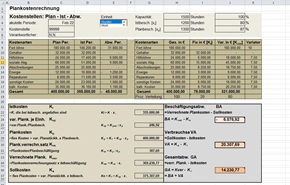





 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>