Home / Fachinfo / Kostenrechnung

Trennung der Kosten in fixe und variable Bestandteile

Dipl. Volkswirt Friedrich Schnepf
Die Durchführung der Teilkostenrechnung setzt die Trennung der Kosten in fixe und variable Bestandteile voraus. Hierzu gibt es verschiedene Verfahren:

Differenzen-Quotienten-Verfahren

Das Differenzen-Quotienten-Verfahren kann angewandt werden, wenn zu zwei verschiedenen Ausbringungsmengen die zugehörigen Gesamtkosten bekannt sind, Es lässt sich dann zunächst auf die variablen Stückkosten schließen und anschließend kann die Höhe der Fixkosten ermittelt werden.

Beispiel:

In der Periode 1 wurden 1.000 Outputeinheiten hergestellt, hierbei entstanden Kosten von 10.000 €. In der Periode 2 wurden 1.200 Outputeinheiten bei Kosten von 11.000 € produziert.

Eine Outputänderung von 200 Einheiten führte also zu einer Kostenänderung von 1.000 €. Daraus folgt, dass jede einzelne Outputeinheit eine Kostenänderung von 1.000 / 200 = 5 € hervorgerufen hat. Die variablen Stückkosten sind also gleich 5 €.

Die variablen Stückkosten können mit Hilfe der folgenden Formel bestimmt werden:

Kv = K2 – K1 = 11.000 – 10.000 = 1.000 = 5
X2 – X1 1.200 – 1.000 200

Bei Betrachtung der Formel wird der Name des Verfahrens einleuchtend: Aus zwei Differenzen wird ein Quotient gebildet.

Die Höhe der Fixkosten lässt sich nun ebenfalls herleiten:

Wenn die variablen Stückkosten 5 € betragen, so betragen die variablen Gesamtkosten bei 1.200 Outputeinheiten 5 * 1.200 = 6.000 €. Da sich die Gesamtkosten bei 1.200 Outputeinheiten auf 11.000 € belaufen, müssen die darin enthaltenen Fixkosten 5.000 € betragen. In Formeln:

K = Kf + Kv * x
11.000 = Kf + 5 * 1.200
11.000 – 6.000 = Kf
 Kf = 5.000

Kritik am Differenzen-Quotienten-Verfahren
  • das Verfahren unterstellt eine lineare Kostenfunktion
  • zufällige Einflüsse machen sich bemerkbar
  • sprungfixe Kosten bleiben unberücksichtigt
  • erhebliche Ungenauigkeiten bei geringer Beschäftigungsdifferenz

Das mathematische Verfahren

Das mathematische Verfahren geht auf Schmalenbach zurück und ist dem Differenzen-Quotienten-Verfahren sehr ähnlich, es gelten auch die gleichen Kritikpunkte wie beim Differenzen-Quotienten-Verfahren. Letztendlich ist das Differenzen-Quotienten-Verfahren lediglich eine Vereinfachung des mathematischen Verfahrens.

Bei Anwendung des mathematischen Verfahrens werden für die beiden oben geschilderten Beschäftigungssituationen die beiden Kostenfunktionen erstellt:
10.000 = Kf + kv * 1.000
11.000 = Kf + kv * 1.200

Durch Umformung der beiden Gleichungen ergibt sich:
Kf = 10.000 – kv * 1.000
Kf = 11.000 – kv * 1.200

Nun dürfen die beiden rechten Seiten der Gleichungen gleichgesetzt werden:
10.000 - kv * 1.000 = 11.000 – kv * 1.200
200kv = 1.000
kv = 5

Die grafische Methode

Die grafische Methode unterstellt wie die mathematische Methode einen linearen Verlauf der Kostenfunktion. Die Beschäftigung und die damit verbunden Kosten werden - jeweils monatlich kumuliert - über ein Jahr hinweg aufgezeichnet. Diese Daten werden in ein Koordinatensystem eingezeichnet. Nun zeichnet man eine Gerade, die möglichst geringe Abstände zu den markierten Kostendaten aufweist. Der Schnittpunkt dieser Geraden mit der Kostenachse gibt die Höhe der Fixkosten an.

Beispiel für zwölf Monate:


 Monatswert kumulierte Werte
Monat Output Kosten Output Kosten
Januar 300 12.800 300 12.800
Februar 500 11.400 800 24.200
März 400 11.000 1.200 35.200
April 700 11.200 1.900 46.400
Mai 900 13.000 2.800 59.400
Juni 500 11.000 3.300 70.400
Juli 300 10.400 3.600 80.800
August 600 11.000 4.200 91.800
September 1.000 12.400 5.200 104.200
Oktober 700 11.200 5.900 115.400
November 500 10.800 6.400 126.200
Dezember 750 11.800 7.150 138.000

Skript08-03-04.gif
Als weitere Methode sei hier noch die Methode der kleinsten Quadrate genannt, die jedoch der grafischen Methode ähnlich ist.




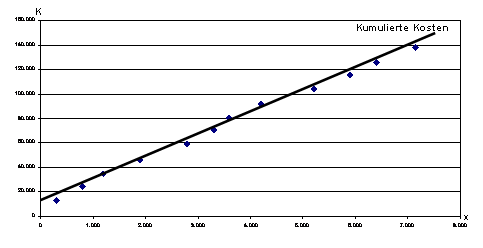
letzte Änderung E.R. am 29.09.2024
Autor:  Dipl. Volkswirt Friedrich Schnepf

Zurück zur Übersicht
Weitere Fachbeiträge zum Thema

Bleiben Sie auf dem Laufenden mit unserem Newsletter

Tragen Sie sich für den kostenfreien und unverbindlichen Newsletter von Controlling-Portal.de ein und erhalten Sie jeden Monat aktuelle Neuigkeiten für Controller. Wir informieren Sie über neue Fachartikel, über wichtige News, aktuelle Stellenangebote, interessante Tagungen und Seminare. Wir empfehlen Ihnen spannende Bücher und geben Ihnen nützliche Excel-Tipps. Verpassen Sie nie mehr wichtige Diskussionen im Forum und stöbern Sie in Software-Angeboten, die Ihnen den Arbeitsalltag erleichtern. Beispiel-Newsletter >>

Jetzt Newsletter gratis erhalten

Premium-Stellenanzeigen



Eigenen Fachbeitrag veröffentlichen? 

Sie sind Autor einer Fachpublikation oder Entwickler einer Excel-Vorlage? Gern können Sie sich an der Gestaltung der Inhalte unserer Fachportale beteiligen! Wir bieten die Möglichkeit Ihre Fachpublikation (Fachbeitrag, eBook, Diplomarbeit, Checkliste, Studie, Berichtsvorlage ...) bzw. Excel-Vorlage auf unseren Fachportalen zu veröffentlichen bzw. ggf. auch zu vermarkten. Mehr Infos >>

Kommentar zum Fachbeitrag abgeben

Nur registrierte Benutzer können Kommentare posten!

Controlling- Newsletter

Neben aktuellen Neuigkeiten für Controller und neu eingegangene Fachartikel, informieren wir Sie über interessante Literaturtipps, Tagungen , Seminarangebote und stellen Ihnen einzelne Software- Produkte im Detail vor.
Werden Sie jetzt monatlich über neue Fachbeiträge, Controlling-Tools und News informiert! Zur Newsletter-Anmeldung >>

Über 3.000 Artikel und Vorlagen

Community_Home.jpg






Werden Sie Mitglied in einer großen Controller-Community (fast 12.000 Mitglieder!) und erhalten Zugriff auf viele Inhalte und diskutieren ihre Fragen im Controlling-Forum.

Sehen Sie hier die neuesten Fachbeiträge >>
Anzeige
RS Controlling System

Eine neue Stelle?

Mit dem Studium fertig, Umzug in eine andere Region, Aufstiegschancen nutzen oder einfach nur ein Tapetenwechsel? Dann finden Sie hier viele aktuell offene Stellen im Controlling.
Zu den Stellenanzeigen >>

Zukunft_Aussicht_Menschen_Fernglas_pm_prometeus_315.jpg

Sie suchen einen Controller? Mit einer Stellenanzeige auf Controlling-Portal.de erreichen Sie viele Fachkräfte. weitere Informationen >>

Controller- Stellenmarkt

Controller (m/w/d), P. W. Lenzen GmbH & Co. KG, Iserlohn
Senior Investment Controller (m/w/d) Investment Reporting und Controlling, L & L Family Office GmbH, Haiger
Mitarbeiter (m/w/d) Kaufmännisches Controlling, Mathias Stiftung, Rheine
Kaufmännischer Leiter (m/w/d), BRUNATA-METRONA GmbH & Co. KG, Ulm, München, Schelklingen
Inhouse Consultant / ERP Finance & Controlling (m/w/d), Beckhoff Automation GmbH & Co. KG, Verl
Controller im Team Finanzen (m/w/d), EPPLE Holding GmbH, Heidelberg
Kaufmann / Kauffrau (w/m/d) als Bilanzbuchhalter / Steuerfachwirt (w/m/d), Energie Südbayern GmbH, München
Controller (m/w/d), MESSRING GmbH, Gilching

Alle Einträge Neuer Eintrag

KLR-Begriffe von A bis Z

A-C   D-F   G-I   J-L   M-R   S-U   V-Z 

Testen Sie ihr Wissen mit unseren Aufgaben und Lösungen im Bereich Kostenrechnung >>

Sie haben eine Frage?

Ratlos_Verwirrt_pm_RainerPlendl_400x275.jpg

Nutzen Sie kostenfrei das Forum für Controller und und diskutieren ihre Fragen zu Controlling-Themen.

Controlling-Software

BusinessPlanner* - Software für Finanzplanung
hmd.rewe - Die integrierte Software für Rechnungswesen
SWOT Controlling
LucaNet Konsolidierungssoftware
LucaNet Finanzplanungssoftware
Diamant/4 Rechnungswesen+Controlling
Serviceware Performance
Alle Einträge Neuer Eintrag

Riesen- Ressource

Auf Controlling-Portal.de sind bereits über 1.500 Fachbeiträge veröffentlicht und ständig kommen neue dazu.

Zu den neuesten Fachbeiträgen >>
Zu den derzeit meistgelesenen Fachbeiträgen >>
Zu den Premium-Beiträgen >>

Sie möchten auch einen Fachbeitrag hier veröffentlichen? Dann erhalten Sie hier weitere Informationen >>

Neueste Excel-Vorlagen

Excel-Arbeitshilfe: Kapitalbedarfsplanung und Finanzierungsmix
Dein Finanzplaner in Excel – Deine Finanzen auf einem Blick!
Excel-Arbeitshilfe: Maschinenkosten abhängig von der Auslastung berechnen
Excel-Tool "doppelte Buchführung" für Buchhaltungs-Übungen
Excel Prompt Generator – Erstellen Sie professionelle KI-Prompts in Sekunden!
MS Access Lösung: CRM Kundendatenbank
MS Access Lösung: CRM Kundendatenbank für Energiehandel
Berechnung Einkommensteuer 2007 - 2026 - Excel-Vorlage
Darlehensrechner Annuitätendarlehen - Excel Vorlage
Arbeitstage für einen Zeitraum automatisch berechnen - Excel-Vorlage
Alle Einträge Neuer Eintrag

Amüsante Glosse

Zweifel_Denken_Frau_Brille_pm_luckyraccoon_400x300.jpg

Erfolgreiche Unternehmer einer Kleinstadt treffen sich regelmäßig im örtlichen Golfclub und diskutieren mit Ihrer Lieblingskellnerin und BWL-Studentin Pauline betriebswirtschaftliche Probleme. Amüsant und mit aktuellem Bezug geschrieben von Prof. Peter Hoberg.

Zur Serie "Neulich im Golfclub" >>

News

Gehaltsreport: 80.000 Euro Jahreseinkommen reichen für die Top 10 %
„AI Office of the CFO“: Payhawk automatisiert Finanzprozesse mit KI
Sind Unternehmen reif für Generative AI? - Gratis-Online-Bewertung des Status Quo
Vier Trends, die Arbeit nachhaltig verändert haben
87 Prozent der CFOs in Deutschland haben volles Vertrauen in ihre Finanzzahlen
Nachfrage nach Finanz-Experten kühlt ab
Gehaltsübersicht 2025: Controller und Buchhalter weiterhin stark gesucht
Arbeitnehmende schätzen kleine und mittelständische Unternehmen

Sie möchten sich weiterbilden?

mann-treppe-up-karriere_pm_pressmaster_B10716345_400x300.jpg

In unserer Seminar-Rubrik haben wir einige aktuelle Seminar- und Kurs-Angebote für Controller, u.a. auch Kurse zum Controller / IHK zusammengestellt.

Premium-Mitgliedschaft

Erhalten Sie Zugriff auf Premium-Inhalte von Controlling-Portal.de und Rechnungswesen-Portal.de. Aktuelle und ständig erweiterte Fachbeiträge. Verschaffen Sie sich hier einen Überblick über unsere Premium-Inhalte.

Mitgliedschaft wahlweise für nur 119,- EUR für ein Jahr, 199,- für 2 Jahre oder 399,- für 5 Jahre Laufzeit! Studenten und Auszubildende 39,- EUR für zwei Jahre! Kein Abonnement! Weitere Informationen >>
 

Wie zufrieden sind Sie mit uns?

Über Ihre Meinung und auch ihre Anregungen für Veränderungen oder Erweiterungen würden wir uns sehr freuen. Nur 10 kurze Fragen, die schnell beantwortet sind. Vielen Dank im Voraus für Ihre Mithilfe! zur Umfrage >>
 

Jobletter und Newsletter!

Mit dem monatlich erscheinenden Newsletter werden Sie über neue Fachbeiträge, News und Excel-Tools informiert! zur Anmeldung >>

Der 14-tägige Jobletter informiert Sie automatisch über neue Stellenangebote und Arbeitsmarkt-News! zur Anmeldung >>
 

Fachbeitrag veröffentlichen?

Sie sind Autor von Fachbeiträgen mit Controlling-bzw. Rechnungswesen-Thema? Gerne veröffentlichen oder vermarkten wir ihren Fachbeitrag. Eine kurze Autorenvorstellung oder Unternehmensdarstellung am Ende des Artikels ist möglich. jetzt Mitmachen >>

Talentpool - Jobwechsel einfach!

HR-Bewerbung-Digital_pm_yupiramos_B123251108_400x300.jpg

Tragen Sie sich kostenfrei im Talentpool auf Controlling-Portal.de ein und erhalten Jobangebote und Unterstützung beim Jobwechsel durch qualifizierte Personalagenturen.

Buch-Vorstellungen


Kennzahlen-Guide

Kennzahlen-Guide-klein.pngÜber 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT.
Jede Kennzahl wird in diesem Buch ausführlich erläutert. Neben der Formel wird eine Beispielrechnung aufgeführt. Für viele branchenneutrale Kennzahlen stehen Zielwerte bzw. Orientierungshilfen für eine Bewertung zur Verfügung. Für die genannten Bereiche hat die Redaktion von Controlling-Portal.de jeweils spezialisierte Experten als Autoren gewonnen, die auf dem jeweiligen Gebiet über umfangreiche Praxiserfahrung verfügen. 

Preis: ab 12,90 Euro Brutto  mehr Informationen >>
 

Dashboards mit Excel

dashboards_cover.jpgWie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.

Taschenbuch in Farbe für 34,90 EUR
oder E-Book für 12,90 EUR 
mehr Informationen >>

  

Reporting 1x1

reporting1x1-klein.jpgViel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.

Taschenbuch in Farbe für 24,90 EUR
oder E-Book für 15,90 EUR 
mehr Informationen >>

Anzeige

Wie zufrieden sind Sie mit uns?

teamwork_pm_Dmitriy_Shironosov_400x300.jpg  
Über Ihre Meinung und auch ihre Anregungen für Veränderungen oder Erweiterungen würden wir uns sehr freuen. Nur 3 kurze Fragen, die schnell beantwortet sind. Vielen Dank im Voraus für Ihre Mithilfe! zur Umfrage >>

Controlling-Software gesucht?

controlling_Dashboard_pm_ml12nan_B9707546_400x300.jpg

Verschaffen Sie sich hier einen Überblick >>
Anzeige
Excel-Vorlagen für Controlling und Rechnungswesen

Stellenanzeigen

Controlling-Spezialist (m/w/d)
Wir sind ein zukunftsorientiertes, modernes Entsorgungsunternehmen mit ca. 200 Mitarbeitern. Mit unserer 50-jährigen Erfahrung steht die MEAB als öffentliches Unternehmen der Bundesländer Brandenburg und Berlin für einen verantwortungsvollen Umgang mit Abfällen. Wir erbringen für Akteure aus Indu... Mehr Infos >>

Office Manager & Personal Assistant (w/m/d)
Die WHU – Otto Beisheim School of Management ist die renommierteste private Hochschule in Deutschland und genießt auch international hohes Ansehen. Unsere Standorte in Vallendar und Düsseldorf bieten ein spannendes und sehr internationales Arbeitsumfeld. Die Kultur an der WHU ist geprägt von unte... Mehr Infos >>

Teamleitung Finanzbuchhaltung (m/w/d)
Sie sind ein versierter Zahlenexperte mit Führungstalent und suchen eine Aufgabe, in der Ihr Können wirklich geschätzt wird? Das bieten wir Ihnen: Polstermöbel Fischer zählt mit rund 250 Mitarbeitenden zu den großen Polstermöbel-Filialunternehmen in Deutschland mit dem Ziel die Nr. 1 zu sein! Wir... Mehr Infos >>

(Production) Controller (m/w/d)
Unsere ausgeprägte Leidenschaft für Live Entertainment, Musicals und Theateraufführungen auf höchstem Niveau ist, was uns bei Stage verbindet. Diese gemeinsame Begeisterung macht aus den vielfältigsten Mitarbeitenden in unterschiedlichsten Jobs ein hingebungsvolles Team: ein echtes „Wir“. Und das... Mehr Infos >>

Leitung (m/w/d) für den Bereich „Finanzmanagement und Controlling“
Das Helmholtz-Zentrum Hereon betreibt internationale Spitzen­forschung für eine Welt im Wandel: Rund 1.000 Beschäftigte leisten ihren Beitrag zur Bewältigung des Klimawandels, der nachhaltigen Nutzung der welt­weiten Küsten­systeme und der ressourcen­verträglichen Steigerung der Lebens­qualität. ... Mehr Infos >>

Kaufmann / Kauffrau (w/m/d) als Bilanzbuchhalter / Steuerfachwirt (w/m/d)
Die Energie Südbayern (ESB) bildet ge­mein­sam mit den Tochter­unter­nehmen Energie­netze Bayern und der ESB Wärme die ESB-Unter­nehmens­gruppe. Mit rund 450 Mit­arbeite­rinnen und Mit­arbeitern, Aus­zu­bil­den­den und Trainees stehen wir für leistungs­fähigen Service, flexible Energie­pr... Mehr Infos >>

(Junior) Business Partner* Controlling
Du hast Lust in einer Mannschaft zu arbeiten, für die partnerschaftliches Miteinander an erster Stelle steht? Mit Menschen, die genauso viel Freude an ihrer Arbeit haben wie du? Dann komm zu uns. Die Paul Bauder GmbH & Co. KG in Stuttgart ist seit über 160 Jahren inhabergeführt und Europas führen... Mehr Infos >>

Controller (m/w/d)
MESSRING ist Branchenführer für Crashtest-Technologie. Seit mehr als fünf Jahrzehnten machen wir mit unseren Produkten und Dienstleistungen Mobilität sicherer – und das weltweit. Unsere Systeme ermöglichen es Unternehmen, Transportmittel zu entwickeln, die Menschen schützen und Leben im Straßenve... Mehr Infos >>

Weitere Stellenanzeigen im Stellenmarkt >>

Folgen Sie uns!

panthermedia_B90564160_patronestaff_310px.jpg

Controlling-Portal auf:
Facebook >> und  Linkedin >>

Viele kostenlose Webinare rund ums Controlling

CoPlanner_Logo_2_RGB_tuerkis_300dpi-controllingportal.jpg
In unseren Webinaren erfahren Sie, wie Sie Ihr Controlling auf ein neues Niveau heben. Neueste Trends, praxisnahe Einblicke und wie Sie Ihre Fähigkeiten optimieren können.  Vom präzisen Forecasting über HR-Controlling bis zur Konsolidierung und integrierten Planung: Die Webinare sind darauf ausgerichtet, Sie zu inspirieren, zu informieren und zu befähigen.     Mehr Infos >>  

JOB- TIPP

Karriere_290px.png
Sind Sie auf der Suche nach einer neuen Herausforderung? Interessante Stellenangebote für Controller finden Sie in der Controlling-Portal Stellenbörse. Immer auf dem Laufenden bleiben und neue Jobangebote mit dem Jobletter automatisch erhalten? Zur Jobletter-Anmeldung >>

Excel-Tool Plankostenrechnung

Plankostenrechnung mit IST-Abweichung.jpg
Nach Eingabe der Plankosten und Ist-Kosten für eine Kostenstelle und Periode, sowie der Aufteilung der Kosten in variable und fixe Kosten, werden formelgestützt alle relevanten Größen (Sollkosten, verrechnete Plankosten etc.) ermittelt und eine Abweichungsanalyse (rechnerisch und grafisch) durchgeführt.

Jetzt hier für 25,- EUR downloaden >>

Excel-Tools für Controller!

Diagramme_Charts_pm_chormail@hotmail-com_B347361660_400x300.jpg

Über 500 Vorlagen direkt zum Download. Verschaffen Sie sich einen Überblick >>

Software-Tipps

LucaNet_simply_intelligent_Logo_RGB.jpg
LucaNet.Financial Consolidation ist die Software für eine prüfungssichere Konsolidierung, die alle Funktionen für die Erstellung eines legalen Konzernabschlusses nach unterschiedlichen Rechnungslegungsstandards bietet.
Mehr Informationen >>

Weitere Controlling-Software-Lösungen im Marktplatz >>

Excel-Vorlage SWOT Analyse Dashboard

SWOT-Analyse-mit-Excel.png
In dieser Excel-Vorlage können Sie 4 verschiedene Charts individuell pro Bereich der SWOT Analyse auswählen. Wenn diese zum Einsatz kommt, ist es sehr hilfreich, professionelle Business-Charts zu erstellen, um die jeweilige Situation besser darzustellen.
Mehr Informationen >>

ETF-Rechner

Der ETF-Rechner vergleicht die mögliche Wertenwicklung von ausschüttenden und thesaurierenden Aktien-ETFs zu den eingegebenen Annahmen. Das Excel-Tools funktioniert wie ein Zinseszinsrechner, optimiert auf ETFs!
Mehr Informationen >>

RS Controlling-System für EÜR inkl. Liquiditätsplanung

RS Controlling System.png
Mit dem RS-Controlling-System für Einnahme-Überschuss-Rechnung steuern Sie erfolgreich ihr Unternehmen. Dieses Tool ermöglicht es Ihnen ihr Unternehmen zu planen, zu analysieren und zu steuern. Durch den Soll-/Ist-Vergleich für Ihre Einnahmen-Überschuss-Rechnung können Sie gezielt  Abweichungen analysieren. 
Mehr Informationen >>

Weitere über 400 Excel-Vorlagen finden Sie hier >>

Premium-Inhalte

Als Premium-Mitglied erhalten Sie Zugriff auf ausgewählte sonst kostenpflichtige Fachbeiträge und Video-Kurse für Premium-Mitglieder inklusive (über 400 Beiträge allein auf Controlling-Portal.de + Premiuminhalte auf Rechnungswesen-Portal.de).

Beispiele:

- Serie zum Berichtswesen in Unternehmen
- Kundenwertanalyse – Wie profitabel ist ein Kunde?
- Potenzialanalyse mit Excel
- Unsere amüsante Glosse: Neulich im Golfclub
- Kostenmanagement in der Logistik
- Dashboards im Kostenmanagement
- Von Total Cost of Ownership (TCO) zu TCOplus
- KLR - Aus der Praxis für die Praxis

Die Gesamtliste an Premium-Fachbeiträgen können Sie hier einsehen >>

Excel TOP-SellerRS Liquiditätsplanung L

PantherMedia_pannawat_B100513902_400x300.jpg
Die RS Liquiditätsplanung L ist ein in Excel erstelltes Werkzeug für die Liquiditätsplanung von Kleinunternehmen sowie Freiberuflern. Die Planung erfolgt auf Basis von veränderbaren Einnahmen- und Ausgabepositionen. Detailplanungen können auf extra Tabellenblättern für z.B. einzelne Projekte oder Produkte vorgenommen werden. 
Mehr Informationen >>

Rollierende Liquiditätsplanung auf Wochenbasis

Dieses Excel-Tool bietet Ihnen die Grundlage für ein Frühwarnsystem. Der erstellte Liquiditätsplan warnt Sie vor bevorstehenden Zahlungsengpässen, so dass Sie frühzeitig individuelle Maßnahmen zur Liquiditätssicherung einleiten können. Gerade in Krisensituationen ist eine kurzfristige Aktualisierung und damit schnelle Handlungsfähigkeit überlebenswichtig. Mehr Informationen >>

Strategie-Toolbox mit verschiedenen Excel-Vorlagen

Die Strategie-Toolbox enthält 10 nützliche Excel Vorlagen, die sich erfolgreich in der Strategie bewährt haben. Alle Tools sind sofort einsatzbereit und sind ohne Blattschutz. Damit können die Vorlagen individuell angepasst werden.
Ideal für Mitarbeiter aus dem strategischen Management. Mehr Informationen>>

Weitere über 400 Excel-Vorlagen finden Sie hier >>

Software-Tipp

Liquiditätsplanung_Fimovi.jpgRollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>