Kybernetik und Controlling

Der Terminus „Controlling“ leitet sich bekanntlich aus dem englischen Verb „to control“ ab, was richtigerweise mit „steuern“, „zielgerichtet Einfluss nehmen“ u. ä. zu übersetzen ist und implizit auch „kontrollieren“ mit einschließt.

So interpretiert, kann ein Zusammenhang zwischen „Controlling“ und „Kybernetik“ sofort hergestellt werden, denn unter Kybernetik ist die Wissenschaft von den allgemeinen Funktionsprinzipien, Strukturen und Gesetzmäßigkeiten der Steuerung dynamischer Systeme unterschiedlicher materieller Beschaffenheit zu verstehen, womit auch der Bereich der Wirtschaft und damit das Aufgabengebiet der Steuerung der Wirtschaftstätigkeit von Unternehmen über das Management eingeschlossen ist. [1]

Damit liegt folgende Frage auf der Hand: In welcher Weise kann sich die Kenntnis allgemeingültiger kybernetischer Aussagen und Modelle für die Ausgestaltung des Controllings in Unternehmen und bei der Vermittlung bzw. Aneignung von Controlling-Wissen als produktiv und nützlich erweisen? Mit diesem Beitrag möchte der Autor anhand eines ausgewählten aktuellen Sachverhalts verdeutlichen, wie die Denkweise und das methodische Herangehen der Kybernetik neue Impulse für „klassische“ Aufgaben im Bereich von Kostenrechnung und Controlling zu liefern vermag. Dabei wird von folgender aktueller betriebswirtschaftlichen Situation ausgegangen:

Seit geraumer Zeit haben die Unternehmen in allen Branchen mit wesentlich veränderten Rahmenbedingungen für den Vollzug ihrer Wirtschaftstätigkeit zu kämpfen. Besonders hervorzuheben sind hier die Auswirkungen, die sich aus

• der beträchtlichen Erhöhung der Preise für Energie, Rohstoffe und andere Inputgüter, 
• den unzuverlässiger werdenden Lieferketten und auch 
• aus Beschränkungen in der generellen Beschaff- bzw. Verfügbarkeit bei wichtigen Inputgütern

ergeben.

Was können bzw. sollen Unternehmen somit in dieser Situation tun? Aus Controller-Sicht kann eine Antwort auf diese Frage etwa wie folgt lauten:

Konzentrieren wir uns (im betreffenden Unternehmen) in einem ersten Schritt darauf, die kostenseitigen Folgen von Preissteigerungen bzw. Verfügbarkeitsbegrenzungen bei den kritischen Einsatzfaktoren im Betriebsprozess im Hinblick auf die die wirtschaftliche Lage des Unternehmens transparent zu machen! Mit anderen Worten:

Es gilt also zu analysieren und aufzuzeigen, welche Auswirkungen eine zahlenmäßige (quantitative) Veränderung des Preises P_i bei einem Einsatzfaktor F_i um einen Betrag von +- ΔP_i auf die Höhe der produktbezogenen variablen Kosten kv, k im Sinne von + - Δk_{v, k} bei den erstellten bzw. zu fertigen Erzeugnissen E_k hat bzw. haben kann. Analog dazu geht es des Weiteren darum, sichtbar zu machen, wie sich eine Verknappung der verfügbaren Menge bei einem Einsatzfaktor F_i um einen zu quantifizierenden Betrag von -Δm_i auf die mögliche Ausstoßmenge q_k bei einem Erzeugnis E_k auswirken wird.

Um ein mögliches Vorgehen bei einer derartigen Untersuchung zu demonstrieren und hierbei den nutzbaren methodischen Beitrag kybernetischer Modellansätze aufzuzeigen, wird in diesem Beitrag die aus dem Kosten-Controlling bekannten Vorgehensweise der Analyse von Kostenabweichungen nach der flexible Plankostenrechnung genutzt.

Konzept der „klassischen“ Analyse von Kostenabweichungen

Folgende Beispiel-Situation bilde den Ausgangspunkt der Untersuchungen: Für eine Hauptkostenstelle in einem Industrie-Unternehmen wurden mit Hilfe von Plankostenverrechnungssätzen die Plankosten für den Zeitraum eines Monats ermittelt. Im Ergebnis der Erfassung und Abrechnung der erbrachten Leistung liegen Ist-Kosten vor. Die Ist-Kosten sind - so die Annahme - höher als die Plankosten.

Wir verzeichnen eine Kostenüberschreitung. Was sind nun die Ursachen dieser Überschreitung? Die Antwort auf diese wichtige Frage liefert folgendes allgemeingültige Modell der Abweichungsanalyse (siehe Abb. 1):


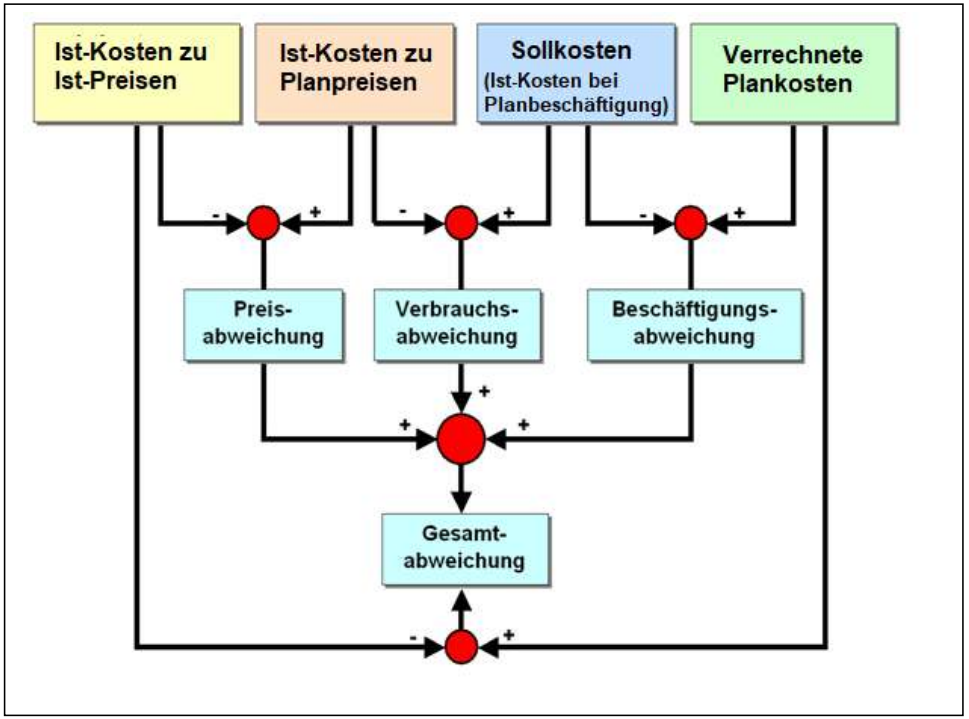Abb. 1: Analyse von Kostenabweichungen mittels flexibler Plankostenrechnung

Gesamtabweichung

Die im Rahmen einer Abweichungsanalyse zu bestimmende kostenseitige Gesamtabweichung ergibt sich aus der Differenz zwischen den Ist-Kosten (berechnet Ist-Mengen zu Ist-Preisen bei Ist-Beschäftigung) und den verrechneten Plankosten (zu Planpreisen bei Ist-Beschäftigung):

1. Formel:

	Ist-Kosten (bei Ist-Beschäftigung und Ist-Preisen) [EUR]
–	verrechnete Plankosten (bei Ist-Beschäftigung und Planpreisen) [EUR]
=	Gesamtabweichung [EUR]

Der Ausweis einer Gesamtabweichung [EUR] ist aber im Hinblick auf eine steuerungsseitige Einflussnahme auf Betriebsprozesse noch wenig aussagefähig. Tiefergehende Erkenntnisse über Ursachen von Kostenabweichungen liefert erst die Ermittlung jener Abweichungsgrößen, die in Abb. 1 angegeben sind und die in ihrer Zusammenführung die Gegenrechnung zur ermittelten Gesamtabweichung verdeutlicht.

Beschäftigungsabweichung

Eine Beschäftigungsabweichung im Kostenausdruck tritt immer dann ein, wenn die Ist-Beschäftigung [h] in einer Kostenstelle von der Plan-Beschäftigung [h] nach oben oder nach unten abweicht. Um diese Abweichung zu bestimmen, werden zunächst jene Kosten ermittelt, die als Plankosten - umgerechnet auf den Ist-Beschäftigungsgrad - anfallen sollten. Diese Kosten werden als sog. Sollkosten bezeichnet. Diese Sollkosten setzen sich zusammen aus

1. den fixen Plankosten, die ja auch dann anfallen, wenn in einer Kostenstelle keine Beschäftigung vorliegt und 
2. den variablen (proportionalen) Kosten, die von der Höhe der jeweiligen Ist-Beschäftigung abhängen.

Die Aufspaltung der Kosten einer definierten Kostenart in fixe und variable Kosten wird im Rahmen der flexiblen Plankostenrechnung mittels einer Hilfsgröße vorgenommen, die auf analytischem Wege als Variator V wie folgt bestimmt werden kann:

2. Formel:

Variator V	=	Kostenänderung [%]	×	10
		10 %-ige Änderung der Planbeschäftigung

Wenn eine Änderung der Beschäftigung um 10 % eintritt, die Kosten K sich jedoch nicht ändern, nimmt die Größe V den Wert V = 0 an; wir haben es wiederum mit rein fixen Kosten zu tun. Zeigt sich aber bei einer Kostenart eine 10 %-ige Änderung der Beschäftigung eine Kostenänderung von beispielsweise 6 % an, dann nimmt V den Wert V = 6 an. Wir haben es in diesem Fall mit Mischkosten zu tun: Der Anteil variabler Kosten beträgt 60 %, der Anteil fixer Kosten beträgt 40 %.

Ist für jede Kostenart der Wert des Variators V bekannt, so können folgende Berechnungen vorgenommen werden:

3. Formel:

variable Kosten einer Kostenart	=	Kosten der Kostenart [EUR] × V	[EUR
		10
fixe Kosten einer Kostenart	=	Kosten der Kostenart [EUR] – variable Kosten der Kostenart	[EUR]

Die Sollkosten bei Ist-Beschäftigung können dann wie folgt ermittelt werden:

4. Formel:

	Summe der Fixkosten [EUR] aller Kostenarten
+	Summe der variablen Kosten [EUR] aller Kostenarten
=	Sollkosten [EUR]

Werden die so ermittelten Sollkosten nun der Summe der verrechneten Plankosten (bei Planbeschäftigung) gegenübergestellt, erhalten wird die Größe der Beschäftigungsabweichung:

5. Formel:

	Summe der verrechneten Plankosten [EUR]
–	Sollkosten [EUR]
=	Beschäftigungsabweichung [EUR]

Die Beschäftigungsabweichung [EUR] weist einen negativen Wert auf, wenn die IstBeschäftigung [h] kleiner als die Planbeschäftigung [h], da in diesem Falle nicht die gesamten Fixkosten auf die gegebene Beschäftigung verrechnet werden konnten. Auftragsstornierungen mit ihren Wirkungen auf die Ist-Beschäftigung würden daher besonders bei jenen Unternehmen zu hohen Werten einer negativen Beschäftigungsabweichung führen, die in den Hauptkostenstellen einen hohen Anteil an Fixkosten aufweisen!

Eine positive Beschäftigungsabweichung ergibt sich logischerweise immer dann, wenn die Ist-Beschäftigung über dem Wert Planbeschäftigung liegt, da dann die Fixkosten auf mehr Leistungsstunden verrechnet werden können.

Verbrauchsabweichung

Eine Verbrauchsabweichung tritt ein, wenn die variablen Istkosten [EUR] bei PlanBeschäftigung [h] von den ermittelten variablen Sollkosten [EUR] bei Plan-Beschäftigung [h] abweichen:

6. Formel:

	variable Sollkosten bei Ist-Beschäftigung [EUR]
–	variable Ist-Kosten bei Planbeschäftigung [EUR]
=	Verbrauchsabweichung [EUR]

Zunächst werden die variablen Sollkosten einer Kostenart ermittelt, indem die proportionalen Plankosten dieser Kostenart (bei Planbeschäftigung) [EUR] mit dem IstBeschäftigungsgrad [%] multipliziert werden:

7. Formel:

variable Sollkosten [EUR]	= variable Plankosten [EUR] ×	Ist-Beschäftigung [%]
		100

Dann werden die variablen Ist-Kosten (bei Ist-Beschäftigung) ermittelt, indem wir von den bekannten Ist-Kosten (gesamt) je Kostenart die nicht vom Beschäftigungsgrad abhängigen Fixkosten (je Kostenart) subtrahieren:

8. Formel:

variable Ist-Kosten [EUR] = Ist-Kosten [EUR] – Fixkosten [EUR]

Die Verbrauchsabweichung hat ihre Ursache in Abweichungen der tatsächlichen Einsatzmengen (Material, Arbeitszeit u.a.) von den geplanten Einsatzmengen, aber auch von der Bewertung der Einsatzmengen mit Preisen (veränderte Materialpreise, Stundenlöhne, Energiepreise u. a.)

Preisabweichung

Eine Preisabweichung ergibt sich dann, wenn die Ist-Kosten zu Ist-Preisen (berechnet aus Ist-Mengen und Ist-Preisen) von den Ist-Kosten zu Planpreisen (berechnet aus Ist-Mengen und Planpreisen) abweichen:

9. Formel:

	Ist-Kosten zu Ist-Preisen [EUR]
–	Ist-Kosten zu Planpreisen [EUR]
=	Preisabweichung [EUR]

Der explizite Ausweis der Höhe der Preisabweichung verdeutlicht - im Unterschied zum Ausweis der Verbrauchsabweichung - den Einfluss externer Faktoren auf die Kostenverursachung im Betriebsprozess. Die Zusammenführung der drei ermittelten Abweichungsgrößen führt in ihrer Addition zur Gesamtabweichung (siehe Abb. 1). Dieses Additionsergebnis muss „auf den Cent“ mit der Abweichungsgröße übereinstimmen, die nach Formel (1) ermittelt wurde.

Bewertung des „klassischen“ Konzepts der Abweichungsanalyse

Das hier erläuterte Konzept zur Analyse von Kostenabweichungen eignet sich in der betriebswirtschaftlichen Praxis in jenen Fällen, in denen es um eine „a-posteriori" [2] - Aufdeckung und Erklärung von nachweislich in Hauptkostenstellen eines Unternehmens eingetretenen Abweichungen der Ist-Kosten zu Plankosten geht.

Wenn jedoch die Aufgabe darin besteht, die möglichen Wirkungen von voraussichtlich eintretenden Veränderungen in Bezug auf die Beschäftigungslage, die Verfügbarkeit von Material, Energie u. a. oder auch in Bezug auf Preise bei benötigten Einsatzfaktoren zu ermitteln und zu bewerten, um daraus Schlussfolgerungen für die Steuerung von Fertigungsprozessen abzuleiten, sollte das hier skizzierte Konzept einer Abweichungsanalyse erweitert werden, und zwar in Richtung von „WAS-WÄRE-WENN …“-Rechnungen!

Hierbei kann die Vorgehensweise der Kybernetik bei der Erstellung von rechenfähigen Modellen für Analyse- und Vorschau-Rechnungen sehr hilfreich sein, wobei die Tabellenkalkulationssoftware MS Excel genutzt werden kann. Eine Beispiel-Datei kann hier kostenfrei heruntergeladen werden >>

Ein kybernetischer Modellansatz für kostenrechnerische Abweichungsanalysen

Das typische - kybernetisch orientierte -. Vorgehen bei der Untersuchung von Ursache-Wirkung-Zusammenhängen in realen Prozessen geht von folgenden Fragestellungen aus (siehe auch Abb. 2):

• Was sind die typischen Output-Größen des zu untersuchenden Prozesses? (Symbol y_k, mit k = 1, 2, …, n); 2 a-posteriori = „im-nach-hinein“ 6 
• Was sind die typischen Input-Größen des zu untersuchenden Prozesses? (Symbol x_i, mit i = 1, 2, …, m); 
• Was sind jene Übertragungs- bzw. Transformationsfaktoren T_k,i, die den Zusammenhang zwischen einer Output-Größe y_k und einer Inputgröße x_i in einer Rückwärtsrechnung qualitativ und quantitativ beschreiben und welchen Inhalt haben diese Größen als Übertragungs- bzw. Transformationsfaktoren T_i,k, die in einer Vorwärtsrechnung den Zusammenhang einer Input-Größe x_i und einer OutputGröße y_k kennzeichnen?

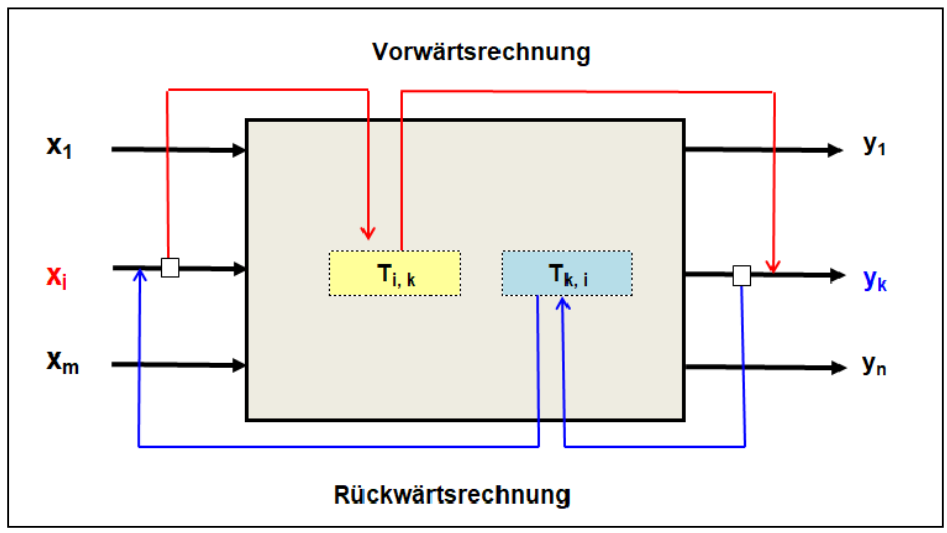Abb. 2: Allgemeiner kybernetischer Modellansatz

Dieser allgemeine Modellansatz wird in einem Fallbeispiel zur Abweichungsanalyse in folgender Weise interpretiert: Gegenstand der Modellbildung unter dem Aspekt einer kostenrechnerischen Abweichungsanalyse ist - wie angegeben - eine Hauptkostenstelle in einem Industrie-Unternehmen.

Einzige Output-Größe y_k sei die im Zeitraum eines Monats laut Plan zu erstellende Menge an einem Vor-, Zwischen- oder Haupterzeugnis E (Output-Größe q [EE]). Diese Größe ist die Ausgangsgröße für die Rückwärtsrechnung, die mit dem Ziel durchgeführt wird, jene zur Absicherung der Output-Größe erforderlichen Mengen an prozessbedingten Input-Größen zu ermitteln.

Als derartige Input-Größen werden in diesem Fallbeispiel betrachtet:

• Arbeitszeit [h] der nach Fertigungslohn Beschäftigten (Symbol AzFL), 
• Arbeitszeit [h] der nach Hilfslohn Beschäftigten (Symbol AzHL), 
• eine ausgewählte Position Fertigungsmaterial [ME] als unabdingbare Prozessvoraussetzung (Symbol FM), 
• Energie (Strom) [kWh] (Symbol EnS), 
• Energie (Gas) [kWh] (Symbol EnG).

Um - ausgehend von einer geplanten Menge q der Output-Größe - über eine Rückwärtsrechnung die benötigten Mengen an den jeweiligen Input-Größen ermitteln zu können, werden Angaben zu den Transformationsfaktoren T_k,i benötigt. Dem betriebswirtschaftlichen Inhalt nach handelt es sich im betrachten Fall um folgende Transformationsfaktoren:

1. Arbeitszeitintensität in Bezug auf die Fertigungslohnstunden (Symbol azi [h/EE])

Formelansatz (10. Formel): AzFL = azi × q [h]

Die so ermittelte Arbeitszeit entspricht dann der Planbeschäftigung nach dem Konzept der klassischen Kostenstellenrechnung.

2. Materialintensität in Bezug auf das Fertigungsmaterial (Symbol mi [ME/EE])

Formelansatz (11. Formel): FM = mi × q [ME]

3. Energieintensität in Bezug auf den Stromverbrauch (Symbol eniS [kWh/EE])

Formelansatz (12. Formel): EnS = eniS × q [kWh]

4. Energieintensität in Bezug auf den Gasverbrauch (Symbol eniG [kWh/EE])

Formelansatz (13. Formel): EnG = eniG × q [kWh]

Die benötigte Arbeitszeit der nach Hilfslohn Beschäftigten wird im Fallbeispiel über einen Anteilsfaktor f_HL mit Bezug zur Arbeitszeit nach Fertigungslohnstunden ermittelt:

Formelansatz (14. Formel): AzHL = AzFL × f_HL [h].

Für die Ermittlung der Plankosten werden im Weiteren die jeweiligen Planpreise P_i (in [EUR/h bzw. in EUR/ME bzw. in EUR/KWh]) für die benannten Input-Größen benötigt. Für eine Differenzierung der Plankosten nach den Anteilen „variable Kosten“ und „fixe Kosten“ sind bei den Input-Größen des Weiteren noch die Variatoren V_i zu bestimmen. Mit all diesen Angaben kann die Plankostenrechnung - als Rückwärtsrechnung - abgeschlossen werden.

Das Problem, das in diesem Beitrag jedoch erörtert werden soll, betrifft die Ermittlung der kostenseitigen Folgen für den Fall, dass sowohl

1. im Vorfeld der Kostenplanung als auch 
2. im Zeitraum der Durchführung des Betriebsprozesses damit zu rechnen ist, dass in Bezug auf die Input-Größen sowohl mit Preiserhöhungen als auch mit Verfügbarkeitsverknappungen gerechnet werden muss bzw. derartige Wirkungen tatsächlich eintreten. 

Um in einem solchen Fall die Auswirkungen sowohl auf die Output-Größe (Produktionsmenge) als auch auf die gesamte Kostensituation in der betreffenden Kostenstelle zahlenmäßig ausweisen zu können, ist eine entsprechende Vorwärtsrechnung - als Engpassrechnung - mit anderen Transformationsfaktoren durchzuführen (siehe Abb. 2).

Diese Transformationsfaktoren ergeben sich rechnerisch als Reziprokwerte der in den Formeln (10) bis (13) angegebenen Intensitätsgrößen und stellen inhaltlich Produktivitätsfaktoren dar Aus der Arbeitszeitintensität azi [h/EE] wird mit 1/azi die Größe Arbeitsproduktivität ap [EE/h], aus der Materialintensität mi [ME/EE] wird mit 1/mi die Materialproduktivität mp [EE/ME], aus der Energieintensität (Strom) eniS [kWh/EE] wird mit 1/eniS die Energieproduktivität enpS [EE/kWh] und aus der Energieintensität (Gas) eniG [kWh/EE] wird mit 1/eniG die Energieproduktivität enpG [EE/kWh].

Werden nun bei den Input-Größen die voraussichtlich verfügbaren oder die im Ist gegebenen Mengen eingesetzt, dann ist die Outputgröße q [EE] als Minimum aus den Einzelergebnissen nach folgenden Beziehungen zu ermitteln:

15. Formel:

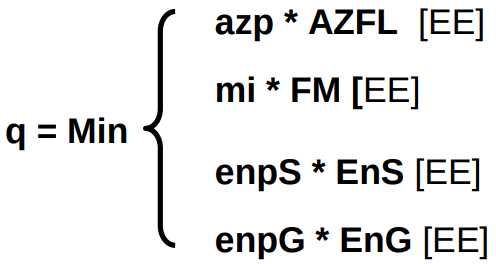
Damit sind zunächst alle formelseitigen Grundlagen für Modellrechnungen angegeben.

Umsetzung in ein kybernetisch orientiertes Simulationsmodell

Das eigentliche Anliegen einer kybernetisch orientierten Abweichungsanalyse in der Kostenstellenrechnung besteht nun nicht darin, eine „a-posteriori“-Analyse nach dem skizzierten klassischen Ansatz nachzuvollziehen, sondern darin, die hier entwickelten Modellansätze für „a-priori“-Simulationsrechnungen im Sinne „WAS-WÄRE-WENN …“ - Rechnungen zu nutzen. Für die praktische Umsetzung dieser Idee kann die Tabellenkalkulationssoftware MS Excel in vorzüglicher Weise genutzt werden. Wie dies umgesetzt werden kann, wird in der beigefügten Excel-Datei

Kyb_Abweichungsanalyse.xlsm

an einem Fallbeispiel demonstriert:

Als Erstes wird der Zusammenhang aller interessierenden Größen - nach dem Muster der Darstellung in Abb. 2 - in ein Blockschaltbild umgesetzt, und zwar einmal für eine Rückwärtsrechnung (als Planungsmodell) und zum anderen für eine Vorwärtsrechnung (als Rechnungsmodell mit Ist-Größen).

Entscheidend ist, dass in beiden Modellen festgelegt wird, welche Modellparameter als Steuerungsgrößen (mit festzulegendem Steuerbereich) in Frage kommen. Für die Steuerung der Modellgrößen kann das in Excel unter dem Menüpunkt „Entwicklungstools/Einfügen“ einsetzbare „Drehfeld“ genutzt werden. Auch kann es sinnvoll sein, die Zellen mit den Modellparametern mit Klartextnamen (Menüpunkt „Formeln/Namen definieren“ zu benennen. Für Erläuterungen kann die Funktion „Kommentare einfügen“ genutzt werden. Die Auswertung von Plan-/Ist-Simulationsrechnungen wird in gesonderten Tabellen nach dem beschriebenen Konzept nach Abb. 1 vorgenommen.

Ein ganz wichtiger Aspekt einer kybernetisch orientierten Simulationsrechnung besteht im Weiteren darin, mit dem Modell eine Reihe von „Empfindlichkeitsanalysen“ (Sensivitätsanalysen) durchzuführen.

Der Grundgedanke solcher Analysen besteht in folgendem Vorgehen:

„Ändere den Wert eines Steuerparameters x um einen Betrag +- Δx und verfolge am Modell, welche - vom Parameter x abhängigen - Größen y sich dann um welchen Betrag +- Δy ändern“.

Aus dieser Beobachtung kann dann abgeleitet werden, wie „ernst“ zum Beispiel Preisveränderungen bei Input-Größen zu nehmen sind bzw. wie sich Begrenzungen der Verfügbarkeit von Input-Größen auf die Output-Größe auswirken bzw. welche externen Einflüsse (Preisänderungen, Verfügbarkeiten) durch Änderungen der Werte von Transformationsfaktoren (Intensitäts- bzw. Produktivitätsgrößen) über Rationalisierungsmaßnahmen abgefangen werden können u. a. m. Wichtig ist ferner, dass über die Vorwärtsrechnung sofort erkennbar wird, welche Input-Größe als Engpass in der Leistungserstellung wirkt und welche Maßnahmen (z. B. über die Verbesserung der zugehörigen Produktivitätsgröße) zur Überwindung dieses Engpasses beitragen können. Weitere Hinweise zur Nutzung des Simulationsmodells sind der angegebenen ExcelDatei zu entnehmen.

In der Publikation

„Arbeitsbuch zu Betriebswirtschaftslehre – Eine Einführung. Wirtschaftskybernetische Modelle mit Excel-basierten Fallbeispielen“ [3]

werden weitere Simulationsmodelle zu ausgewählten Controlling-Themen mit downloadfähigen Excel-Dateien vorgestellt. Die Excel-Datei zu diesem Beitrag kann hier heruntergeladen werden >>


Fußnoten:
[1] Siehe hierzu auch die Webpräsenz https://kybernetik.online, Punkt 2. Wirtschaftskybernetik.
[2] a-posteriori = „im-nach-hinein“
[3] Siegfried von Känel: Arbeitsbuch zu Betriebswirtschaftslehre – Eine Einführung Wirtschaftskybernetische Modelle mit Excel-basierten Fallbeispielen. Springer -Gabler Verlag, Wiesbaden. Link: https://link.springer.com/book/10.1007/978-3-658-27900-4.

letzte Änderung R. am 01.02.2024 Autor:  Prof. Dr. sc. Siegfried von Känel