BAB: Umlageverfahren bei allgemeinen Kostenstellen

Sind nur z.B. nur vier Hauptkostenbereiche im BAB enthalten und sind diese auch nicht weiter untergliedert, handelt es sich um einen so genannten einfachen einstufigen BAB. Wird mindestens ein Kostenbereich in weitere Kostenstellen gegliedert, so spricht man von einem erweiterten einstufigen BAB. Beispielsweise lässt sich der Bereich Fertigung unterteilen in die Kostenstellen Schlosserei, Dreherei, Schreinerei usw..

Werden neben den Hauptkostenstellen auch allgemeine und Hilfskostenstellen umgelegt, so spricht man von einem mehrstufigen BAB. Dies hängt damit zusammen, dass die Verteilung der Kosten in Abhängigkeit von der Art der Kostenstellen in mehreren Stufen erfolgt. 

Beim mehrstufigen BAB werden zunächst die Kosten der allgemeinen Kostenstellen auf alle anderen, also auf Haupt- und Hilfskostenstellen umgelegt. Im nächsten Schritt werden dann die Kosten der Hilfskostenstellen auf die Fertigungshauptstellen verteilt.




Sind in einem Unternehmen allgemeine Kostenstellen umzulegen, so können hierfür die vier im Folgenden an Hand eines Beispiels beschriebenen Verfahren herangezogen werden. Da nun häufiger die Begriffe Primär- und Sekundärkosten benutzt werden, seien diese kurz erläutert:


Das Gehalt des Fertigungsleiters stellt beispielsweise für die Kostenstelle Fertigung Primärkosten dar. Benutzt dieser Fertigungsleiter jedoch ein Fahrzeug der Kostenstelle Fuhrpark, so werden die hierfür in der Kostenstelle Fuhrpark entstandenen Kosten (also Primärkosten für die Kostenstelle Fuhrpark) auf die Fertigungsstelle umgelegt (also Sekundärkosten für die Kostenstelle Fertigung).

Anhand der Daten des folgenden Beispiels werden die vier Umlageverfahren von allgemeinen Kostenstellen erläutert:

In einem Unternehmen sind zur Erfassung und Verrechnung der innerbetrieblichen Leistungen neben den Hauptstellen (K) auch die allgemeinen Kostenstellen (A) eingerichtet.

Für die Kostenstellen gelten folgende Primärkosten:

Kostenstelle	Primärkosten
A1	10.000
A2	20.000
K1	100.000
K2	200.000

Zu ermitteln sind die Sekundärkosten von K1 und K2, wenn

	Kst	LE
A1 400 Leistungseinheiten herstellt, wovon	A2	50
	K1	150
	K2	200
A2 1.000 Leistungseinheiten herstellt, wovon	A1	200
	K1	300
	K2	500

bezogen haben.

Die vier möglichen Umlageverfahren werden nun anhand dieses Beispiels vorgestellt.

1. Stufenleiterverfahren
2. Iterationsverfahren
3. Block- oder Anbauverfahren
4. Mathematisches Verfahren

1. Stufenleiterverfahren

Die allgemeinen Kostenstellen müssen im BAB immer in den ersten Spalten dargestellt werden. Sie stehen also vor den Haupt-, und sofern vorhanden, den Hilfskostenstellen.

Beim Stufenleiterverfahren werden die Primärkosten der ersten allgemeinen Kostenstelle (die allgemeine Kostenstelle, die im BAB am weitesten links steht) auf alle weiteren Kostenstellen entsprechend dem vorgegebenen Verhältnis verteilt. Dann erfolgt die Umlage der nächsten allgemeinen Kostenstelle auf alle nachfolgenden Kostenstellen usw.

Die Primärkosten der allgemeinen Kostenstellen werden also immer nur nach rechts weiterverrechnet. Nicht berücksichtigt werden also Leistungen, die z.B. von A2 an A1 abgegeben werden. Das Verfahren ist dadurch ungenauer, aber wirtschaftlicher in der Durchführung als andere Verfahren.



Bei der Umlage 1 werden die Kosten von A1 im Verhältnis 50 : 150 : 200 auf die empfangenden Kostenstellen umgelegt. Bei der Umlage 2 werden die Kosten im Verhältnis 300 : 500 auf die Hauptkostenstellen umgelegt. Dass auch A1 von A2 Leistungen empfängt, bleibt unberücksichtigt.

2. Iterationsverfahren

Bei diesem Verfahren werden die Kosten der allgemeinen Kostenstellen mit Hilfe eines Näherungsverfahrens auf die Hauptkostenstellen umgelegt. Hierbei wird die gegenseitige Leistungsinanspruchnahme der allgemeinen Kostenstellen untereinander berücksichtigt. Dieses Verfahren führt zu größerer Genauigkeit als das Stufenleiterverfahren, ist jedoch manuell kaum durchführbar.

Schlüssel für A1	12,5 % A2
	27,5 % K1
	50,0 % K2
Schlüssel für A2	20,0 % A1
	30,0 % K1
	50,0 % K2

3. Block- oder Anbauverfahren

Beim Block- oder Anbauverfahren werden die Kosten der allgemeinen Kostenstellen durch die Leistungseinheiten dividiert, die diese an die Hauptkostenstellen abgeben. Auf diese Art ergeben sich Verrechnungssätze pro abgegebener Leistungseinheit. Die auf diese Weise ermittelten Werte werden entsprechend den abgegebenen Leistungen auf die Hauptkostenstellen verteilt. Liefer- und Empfangsbeziehungen der allgemeinen Kostenstellen untereinander bleiben unberücksichtigt. Das Verfahren ist einfach aber ungenau.

A1 gibt an die Hauptkostenstellen 350 Leistungseinheiten ab.

Die Gesamtkosten von A1 belaufen sich auf 10.000 €.

10.000 / 350 = 28,571429

K1 verbraucht 150 Leistungseinheiten, also werden

28,571429 * 150 = 4.286 an Sekundärkosten auf K1 umgelegt.

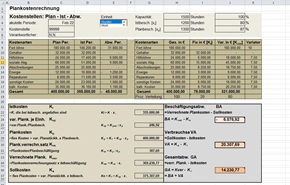
4. Mathematisches Verfahren

Dieses Verfahren ist das exakteste, verursacht aber auch den größten Rechenaufwand. Beim mathematischen Verfahren, auch als Gleichungsverfahren bezeichnet, wird für jede allgemeine Kostenstelle eine Gleichung aufgestellt. Auf der linken Seite der Gleichung werden die von dieser Kostenstelle produzierten Leistungseinheiten dargestellt, während die rechte Seite der Gleichung die primären und sekundären Kosten enthält, die in der Kostenstelle entstanden sind. Gibt es beispielsweise drei allgemeinen Kostenstellen, so entstehen drei Gleichungen mit ebenso vielen Unbekannten. Damit wird das Gleichungssystem lösbar.

Hier noch einmal die Liefer- und Empfangsbeziehungen der Kostenstellen untereinander:

Für die Kostenstellen gelten folgende Primärkosten:

Kostenstelle	Primärkosten
A1	10.000
A2	20.000
K1	100.000
K2	200.000

Zu ermitteln sind die Sekundärkosten von K1 und K2, wenn

	Kst	LE
A1 400 Leistungseinheiten herstellt, wovon	A2	50
	K1	150
	K2	200
A2 1.000 Leistungseinheiten herstellt, wovon	A1	200
	K1	300
	K2	500

bezogen haben.

1. 400 A1 = 10.000 + 200 A2

2. 1.000 A2 = 20.000 + 50 A1

Die Gleichung 1. bringt folgendes zum Ausdruck:

400 Leistungseinheiten der Kostenstelle A1 kosten 10.000 € zuzüglich 200 Leistungseinheiten der Kostenstelle A2. Analoges gilt für die zweite Gleichung. Die Lösung des Gleichungssystems:

A1 = 10.000 / 400 + 200 A2 / 400

A1 = 25 + 0,5 A2

Dies in die Gleichung 2. eingesetzt, ergibt:

1.000 A2 = 20.000 + 50 * (25 + 0,5 A2)
1.000 A2 = 20.000 + 1.250 + 25 A2
975 A2 = 21.250
A2 = 21,80

Dieses Ergebnis wird nun in Gleichung 1 eingesetzt:

400 A1 = 10.000 + 200 * 21,80
400 A1 = 10.000 + 4.360
400 A1 = 14.360
A1 = 35,90

Nun ist bekannt, wie viel eine Leistungseinheit der Kostenstellen A1 und A2 kosten.

	K1	K2
von A1	150 * 35,90 = 5.385	200 * 35,90 = 7.180
von A2	300 * 21.80 = 6.540	500 * 21,80 = 10.900
Sekundärkosten	11.925	18.080

Im dargestellten Beispiel wurde von dem sicher ungewöhnlichen Fall ausgegangen, dass die allgemeinen Kostenstellen von ihren hergestellten Leistungen selbst nichts verbrauchen. Eine Kostenstelle Energie wird jedoch selbst auch Strom verbrauchen, die Kostenstelle Fuhrpark wird auch selbst ihre Fahrzeuge nutzen usw. Im folgenden Beispiel wird nun Eigenverbrauch der Kostenstellen unterstellt.

Für die Kostenstellen gelten folgende Primärkosten:

Kostenstelle	Primärkosten
A1:	8.560
A2:	6.480
K1:	34.757
K2:	195.411
K3:	33.754

Zu ermitteln sind die Sekundärkosten von K1, K2 und K3, wenn

	Kst	LE
A1 600 Leistungseinheiten herstellt, wovon	A1	20
	A2	30
	K1	280
	K2	220
	K3	50
A2 6.000 Leistungseinheiten herstellt, wovon	A1	600
	A2	200
	K1	2.400
	K2	1.800
	K3	1.000

bezogen haben.

Für die Kostenstelle A1 ergibt sich nun folgende Gleichung:

600A1 =8.560 + 600A2 + 20A1

Erläuterung: Sämtliche Kosten der Kostenstelle A1 sollen auf die anderen Kostenstellen umgelegt werden. Die anderen Kostenstellen empfangen von A1 nur 580 LE. Der Eigenverbrauch der Kostenstelle A1 erhöht also die auf die anderen Kostenstellen umzulegenden Kosten und ist deshalb in der Gleichung zu addieren. Als Ergebnis muss die Gleichung liefern, was eine LE von 580 LE kostet.

Für die Kostenstelle A2 wird dann entsprechend folgende Gleichung aufgestellt:

6.000A2 = 6.480 + 30A1 + 200A2

5.800A2 = 6.480 + 30A1







Eine Leistungseinheit (LE) von A1 kostet also 16,00 €. Dieser Wert kann nun für A1 in die Gleichung 2 eingesetzt werden:

6.000A2 = 6.480 + 200A2 + 30 * 16

5.800A2 = 6.960

A2 = 1,2

Eine Leistungseinheit von A2 kostet 1,20 €.

Die innerbetriebliche Leistungsverrechnung (ILV) ergibt folgende Umlagen und Endkosten:

Kosten in €	A1	A2	K1	K2	K3	Summe
Primäre Gemeinkosten	8.560	6.480	34.757	195.411	33.754	278.962
ILV A1 (16,00)		480	4.480	3.520	800	9.280
ILV A2 (1,20)	720		2.880	2.160	1.200	6.960
Endkosten			42.117	201.091	35.754	278.962

Aufgaben zum Kapitel "Umlageverfahren" >>

letzte Änderung E.R. am 29.09.2024 Autor:  Dipl. Volkswirt Friedrich Schnepf