- News
- Forum
- Fachbeiträge
- Grundlagen (95)
- Branchen (49)
- Funktional (91)
- Kostenmanagement (30)
- Konzepte (84)
- Kennzahlen (373)
- Finanzplanung (63)
- Budgetierung (10)
- Reporting / Berichtswesen (35)
- BSC (7)
- Projektcontrolling (17)
- Kostenrechnung (414)
- IAS / IFRS (4)
- Risikomanagement (37)
- Investitionsrechnung (75)
- Unternehmensbewertg. (12)
- Rating (6)
- Business Intelligence (82)
- Excel-Tipps (202)
- Studien (8)
- Arbeitsmarkt (21)
- Spar-Tipps (2)
- Controlling-Journal (23)
- Finanzmathem. Formeln (15)
- Neulich im Golfclub (57)
- Softskills (29)
- Sonstiges (19)
- Artikel-Serien
- Stichwortverzeichnis
- Marktplatz
- Karriere / Stellenmarkt
- Excel-Vorlagen
- Online-Kurse
- Glossar
Äquivalenzziffernkalkulation - Verfahren und Beispiele
Äquivalenzziffernkalkulation (äuqui-valent = gleich-wertig)
Die Äquivalenzziffernkalkulation (Äquivalenzziffernrechnung) ist eine Art der Divisionskalkulation und wird bei einer Sortenfertigung (artgleiche Erzeugnisse) angewendet. Es besteht zwischen den Produktarten ein festes Kostenverhältnis, welches durch Verhältniszahlen (Äquivalenzzahlen) ausgedrückt wird.Die Äquivalenzzahlen zeigen an, in welchem Verhältnis die einzelnen Sorten an der Verursachung der Kosten beteiligt waren. Dieses Kalkulationsverfahren kann in Brauereien, Brennereien, Färbereien, Walzwerke, Ziegeleien angewendet werden.
"Unter Äquivalenzziffern versteht man Verhältniszahlen, die angeben, wie sich die Kostenverursachung der Sorten von den Kosten einer Einheitssorte unterscheiden, der meist die Äquivalenzziffer 1 zugeteilt wird"
Die Äquivalenzziffernrechnung wurde wahrscheinlich in Blechwalzbetrieben eingeführt, die Bleche verschiedener Stärken herstellten. Je dünner das hergestellte Blech war, desto höher war die zugeordnete Äquivalenzziffer, weil die dünneren Bleche höhere Bearbeitungszeiten beanspruchten. Weitere Beispiele für Betriebe, in denen die Äquivalenzziffernrechnung Anwendung findet sind Ziegeleien, die Backsteine unterschiedlicher Größe oder unterschiedlicher Brenndauer herstellen, Brauereien mit mehreren Biersorten, Bonbonfabriken, die aus dem gleichen Grundstoff Bonbons verschiedener Größe herstellen und Sägewerke, die Stämme mit verschiedenen Durchmessern zu unterschiedlich großen Brettern verarbeiten.
Bei der Äquivalenzziffernrechnung lassen sich grundsätzlich vier Verfahren unterscheiden:
- Werden die gesamten Selbstkosten nach einem einzigen Kriterium auf die Erzeugnisse verteilt, so spricht man von einfacher Äquivalenzziffernrechnung.
- Werden für verschiedene Kostenarten oder Kostengruppen (Materialkosten, Fertigungskosten, Verwaltungs- und Vertriebskosten) jeweils eigene Äquivalenzziffern gebildet, so spricht man von differenzierender Äquivalenzziffernrechnung.
- Erfolgt die Herstellung der Produkte in mehreren Produktionsstufen und werden für die verschiedenen Produktionsstufen auch verschiedene Äquivalenzziffern gebildet, so spricht man von mehrstufiger Äquivalenzziffernrechnung.
- Existieren für verschiedene Kostenarten verschiedene Äquivalenzziffern und sind nur die Gesamtkosten des Produktionsprozesses bekannt, so wendet man das multiplikative Verfahren an.
Die Festlegung der Äquivalenzziffern selbst wird meist nach Materialgewicht, Blechstärke, Produktgröße, Gewicht, Längen, Durchmessern, Fertigungszeiten oder ähnlichen technischen oder physikalischen Maßgrößen vorgenommen.
Einfache Äquivalenzziffernrechnung
Für die Anwendung der einfachen Äquivalenzziffernrechnung müssen folgende Voraussetzungen erfüllt sein:- Produzierte und abgesetzte Mengen der Betrachtungsperiode müssen gleich sein, es darf also keine Bestandsänderung bei den Fertigerzeugnissen vorliegen, da dies zu Unterschieden bei den Herstellkosten der Produktion und den Herstellkosten des Umsatzes führen würde.
- Es muss einstufige Produktion vorliegen, oder es dürfen bei mehrstufiger Produktion keine Bestandsveränderungen in den Zwischenlagern auftreten.
- Es müssen sich alle Kosten proportional zu der benutzten Äquivalenzziffer (z. B. zum Gewicht der Produkte) verhalten.
Nur wenn die ersten beiden Voraussetzungen erfüllt sind, lassen sich alle Kosten auf die gleichen Mengen der verschiedenen Sorten beziehen. Die dritte Voraussetzung ist in der Praxis am schwersten zu erfüllen, da es kaum vorstellbar ist, dass sich alle Kosten proportional zu einer einzigen Äquivalenzziffer verhalten. Sollten jedoch alle Voraussetzungen tatsächlich erfüllt sein, so könnte die Kalkulation nach dem folgenden Beispiel erfolgen:
Beispiel zur einfachen Äquivalenzziffernrechnung:
Die Äquizi GmbH stellt aus dem gleichen Material die Produkte A, B und C her. Die drei Produkte unterscheiden sich lediglich hinsichtlich ihres Gewichts: Produkt A wiegt 1,0 kg, Produkt B 1,1 kg und Produkt C 1,2 kg. Das Gewichtsverhältnis der drei Produkte wird der Kostenverteilung zugrunde gelegt.
Diese Angaben werden in eine Tabelle eingetragen, wobei das Gewicht der drei Produkte als Äquivalenzziffer dient:
| Produkt | Produktionsmenge | Äquivalenzziffer |
| A | 360 | 1,0 |
| B | 420 | 1,1 |
| C | 90 | 1,2 |
Nun werden in einer weiteren Spalte die so genannten Verrechnungseinheiten ermittelt, indem die produzierten Mengen der drei Produkte mit ihren Äquivalenzziffern multipliziert werden:
| Produkt | Produktionsmenge | Äquivalenzziffer | Verrechnungseinheiten |
| A | 360 | 1,0 | 360 |
| B | 420 | 1,1 | 462 |
| C | 90 | 1,2 | 108 |
Die ermittelten Verrechnungseinheiten drücken die produzierten Mengen von Produkt B und C in Einheiten des Produktes A aus. Man kann folgende Aussage treffen: Die Produktion von 420 Einheiten des Produktes B wirken sich unter Kostengesichtspunkten so aus, als habe man 462 Einheiten des Produktes A hergestellt. 90 Einheiten des Produktes C entsprechen 108 Einheiten des Produktes A.
Nun ermittelt man die Höhe der Selbstkosten pro Verrechnungseinheit. Insgesamt wurden 930 Verrechnungseinheiten hergestellt. Wenn die Selbstkosten insgesamt 530.100,00 € betragen, ergeben sich die folgenden Selbstkosten pro Verrechnungseinheit:
530.100 / 930 = 570
Nun werden in einer weiteren Tabellenspalte jedem Produkt die von ihm verursachten Gesamtkosten zugeordnet, indem die Anzahl der Verrechnungseinheiten mit den Kosten pro Verrechnungseinheit multipliziert wird.
| Produkt | Produktionsmenge | Äquivalenzziffer | Verrechnungseinheiten | Gesamtkosten |
| A | 360 | 1,0 | 360 | 205.200 |
| B | 420 | 1,1 | 462 | 263.340 |
| C | 90 | 1,2 | 108 | 61.560 |
| Summe |
|
|
930 | 530.100 |
Zur Ermittlung der Stückkosten müssen nun lediglich die Gesamtkosten der drei Produkte durch die produzierten Mengen dividiert werden:
| Produkt | Produktionsmenge | Äquivalenzziffer | Verrechnungseinheiten | Gesamtkosten | Stückkosten |
| A | 360 | 1,0 | 360 | 205.200 | 570 |
| B | 420 | 1,1 | 462 | 263.340 | 627 |
| C | 90 | 1,2 | 108 | 61.560 | 684 |
| Summe |
|
|
930 | 530.100 |
Weiteres Beispiel:
Eine Kerzenfabrik stellt Bienenwachskerzen verschiedener Größe her. Die Kosten richten sich weitgehend nach dem Gewicht der Produkte. Es liegen folgende Daten vor:
| Produkt | Menge | Gewicht (gr) |
| A | 50.000 | 16 |
| B | 100.000 | 20 |
| C | 20.000 | 24 |
| D | 200.000 | 32 |
Gesamtkosten: 726.000 €
Aufgabe:
Kalkulieren Sie die Selbstkosten der verschiedenen Produkte pro Stück.
Lösung:
| Produkt | Menge | ÄZ | VE | K | k |
| A | 50.000 | 16 | 800.000 | 60.000 | 1,2 |
| B | 100.000 | 20 | 2.000.000 | 150.000 | 1,5 |
| C | 20.000 | 24 | 480.000 | 36.000 | 1,8 |
| D | 200.000 | 32 | 6.400.000 | 480.000 | 2,4 |
| Summe |
|
|
9.680.000 | 726.000 |
|
Kosten pro Verrechungseinheit: 726.000 / 9.680 = 0,075
Differenzierende Äquivalenzziffernrechnung
Dieses Verfahren wird immer dann notwendig, wenn für verschiedene Kostenstellen und/oder verschiedene Kostenarten auch unterschiedliche Äquivalenzziffern ermittelt werden können.Beispiel zur differenzierenden Äquivalenzziffernrechnung: (nach Kostenarten)
In einem Betrieb werden die Sorten A, B und C hergestellt. Die Materialkosten belaufen sich auf insgesamt 23.040 €, wobei für die Sorte B 20 % und die Sorte C 30 % mehr Material erforderlich ist als für die Sorte A.
Die drei Sorten beanspruchen eine Maschine im Verhältnis 0,8 : 1 : 1,2. Die maschinenabhängigen Fertigungskosten belaufen sich insgesamt auf 17.930 €. Wie hoch sind die Selbstkosten jeder Sorte und jedes einzelnen Produkts.
Materialkosten:
| Produkt | Menge | ÄZ | VE | K | k |
| A | 100 | 1 | 100 | 6.000 | 60 |
| B | 150 | 1,2 | 180 | 10.800 | 72 |
| C | 80 | 1,3 | 104 | 6,240 | 78 |
| Summe |
|
|
384 | 23.040 |
|
Materialkosten pro Verrechnungseinheit: 23.040 / 384 = 60
Fertigungskosten:
| Produkt | Menge | ÄZ | VE | K | k |
| A | 100 | 0,8 | 80 | 4.400 | 44 |
| B | 150 | 1 | 150 | 8.250 | 55 |
| C | 80 | 1,2 | 96 | 5.280 | 66 |
| Summe |
|
|
326 | 17.930 |
|
Fertigungskosten pro Verrechnungseinheit: 17.930 / 326 = 55
| Produkt | Materialk. / Stück | Fertigungsk. / Stück | Gesamtk. / Stück |
| A | 60 | 44 | 104 |
| B | 72 | 55 | 127 |
| C | 78 | 66 | 144 |
Beispiel zur differenzierenden Äquivalenzziffernrechnung (nach Kostenstellen):
In einem Industriebetrieb werden 5 Sorten hergestellt, die in zwei Fertigungsstellen bearbeitet werden. Es gelten folgende Daten:
| Sorte | Menge | MEK | ÄZ FK1 | ÄZ FK2 |
| 1 | 10.000 | 5,0 | 0,7 | 0,6 |
| 2 | 8.000 | 6,5 | 1,0 | 0,8 |
| 3 | 12.000 | 7,0 | 1,2 | 1,0 |
| 4 | 4.000 | 8,5 | 1,3 | 1,4 |
| 5 | 3.000 | 10,0 | 1,4 | 1,3 |
Es fallen 5 % Materialgemeinkosten an. Die Fertigungskosten der Kostenstelle 1 betragen 97.000 €, die der Fertigungskostenstelle 2 101.700 €. An Verwaltungs- und Vertriebsgemeinkosten sind 10 % auf die Herstellkosten zu berücksichtigen.
Es sind die Fertigungskosten, die Herstellkosten und die Selbstkosten je Stück für die einzelnen Sorten zu bestimmen.
Zunächst werden die Stückkosten der Fertigungsstelle 1 berechnet:
| Sorte | Menge | ÄZ FK1 | VE FK1 | K | kFK1 |
| 1 | 10.000 | 0,7 | 7.000 | 17.500 | 1,75 |
| 2 | 8.000 | 1,0 | 8.000 | 20.000 | 2,50 |
| 3 | 12.000 | 1,2 | 14.400 | 36.000 | 3,00 |
| 4 | 4.000 | 1,3 | 5.200 | 13.000 | 3,25 |
| 5 | 3.000 | 1,4 | 4.200 | 10.500 | 3,50 |
|
|
|
|
38.800 | 97.000 |
97.000 / 38.800 = 2,5
Berechnung der Stückkosten für Fertigungsstelle 2:
| Sorte | Menge | ÄZ FK2 | VE FK2 | K | kFK2 |
| 1 | 10.000 | 0,6 | 6.000 | 18.000 | 1,80 |
| 2 | 8.000 | 0,8 | 6.400 | 19.200 | 2,40 |
| 3 | 12.000 | 1,0 | 12.000 | 36.000 | 3,00 |
| 4 | 4.000 | 1,4 | 5.600 | 16.800 | 4,20 |
| 5 | 3.000 | 1,3 | 3.900 | 11.700 | 3,90 |
|
|
|
|
33.900 | 101.700 |
101.700 / 33.900 = 3,0
Berechnung der Selbstkosten aller Sorten:
| Sorte | Menge | MEK | MGK 5% | FEK 1+2 | HK | VW + VtGK | SK |
| 1 | 10.000 | 5,0 | 0,250 | 3,55 | 8,800 | 0,8800 | 9,6800 |
| 2 | 8.000 | 6,5 | 0,325 | 4,90 | 11,725 | 1,1725 | 12,8975 |
| 3 | 12.000 | 7,0 | 0,350 | 6,00 | 13,350 | 1,3350 | 14,6850 |
| 4 | 4.000 | 8,5 | 0,425 | 7,45 | 16,375 | 1,6375 | 18,0125 |
| 5 | 3.000 | 10,0 | 0,500 | 7,40 | 17,900 | 1,7900 | 19,6900 |
Mehrstufige Äquivalenzziffernrechnung
Durchlaufen die Sorten mehrere Fertigungsstufen und treten Lagerbestandsänderungen in den Zwischenlagern auf, so wird eine mehrstufige Äquivalenzziffernkalkulation erforderlich.Im folgenden Beispiel wird von den 4 Produkten A, B, C und D ausgegangen, die 3 Fertigungsstufen durchlaufen. In jeder Fertigungsstufe treten andere Äquivalenzziffern auf.
| Fertigungsstufe 1 | ||||||
| P | Menge | ÄZ | VE | K | k1 | Lagerbest. |
| A | 100 | 2,00 | 200 | 6.000 | 60,00 | 1.800 |
| B | 150 | 0,70 | 105 | 3.150 | 21,00 | 210 |
| C | 80 | 1,80 | 144 | 4.320 | 54,00 | 540 |
| D | 200 | 1,00 | 200 | 6.000 | 30.00 | 1.200 |
| 649 | 19.470 | 3.750 | ||||
Gesamtkosten d. Fertigungsstufe 1: 19.470
Kosten pro Verrechnungseinheit: 30
| Fertigungsstufe 2 | |||||||
| P | Menge | ÄZ | VE | K | k2 | k1 + k2 | Lagerbest. |
| A | 70 | 1,30 | 91 | 1.502 | 21,54 | 81,45 | 1.629 |
| B | 140 | 1,50 | 210 | 3.465 | 24,75 | 45,75 | 1.830 |
| C | 70 | 1,00 | 70 | 1.155 | 16,50 | 70,50 | 1.410 |
| D | 160 | 1,80 | 288 | 4.752 | 29,70 | 59,70 | 2.388 |
| 659 | 10.874 | 7.257 | |||||
Gesamtkosten d. Fertigungsstufe 2: 10.874
Kosten pro Verrechnungseinheit: 16.50
| Fertigungsstufe 3 | ||||||
| P | Menge | ÄZ | VE | K | k3 | k1+k2+k3. |
| A | 50 | 0,60 | 30 | 990 | 19,80 | 101,25 |
| B | 100 | 1,00 | 100 | 3.300 | 33,00 | 78,75 |
| C | 50 | 0,40 | 20 | 660 | 13,20 | 83,70 |
| D | 120 | 1,10 | 132 | 4.356 | 36,30 | 96,00 |
| 282 | 9.306 | |||||
Gesamtkosten d. Fertigungsstufe 3: 9.306
Kosten pro Verrechnungseinheit: 33,00
Gehen die gleichen Produktmengen in den einzelnen Fertigungsstufen durch Ausschuss statt durch Lagerung verloren, so ergibt sich eine andere Kalkulation:
Die Stückkosten k1+k2+k3 des Produktes A in Fertigungsstufe 3 ergeben sich folgendermaßen:
Es werden also die Gesamtkosten für Produkt A in Fertigungsstufe 1 und Fertigungsstufe 2 addiert und durch die produzierte Menge in Stufe 3 dividiert. Anschließend werden die Stückkosten dieses Produkts in Fertigungsstufe 3 addiert.
Das multiplikative Verfahren
Das multiplikative Verfahren wird angewandt, wenn sich ein Produkt hinsichtlich mehrerer Größen unterscheidet (z.B. eingesetzte Materialmenge, Fertigungszeit), es erfolgt jedoch keine getrennte Erfassung der Material- und Fertigungskosten. Hierbei werden die verschiedenen Äquivalenzziffern miteinander multipliziert und die Berechnung der Selbstkosten erfolgt dann aufgrund des Produktes aus den einzelnen Äquivalenzziffern.Beispiel zum multiplikativen Verfahren:
Ein Betrieb füllt Lebensmittel in 250-g- und 500-g-Dosen ab. Die beiden Dosengrößen werden in der Konservierungsanlage unterschiedlichen Behandlungszeiten unterworfen, um die Haltbarkeitsdauer zu beeinflussen. Dadurch entstehen 4 unterschiedliche Sorten von Dosen. Konservierungszeit und Gewicht können als Äquivalenzziffern verwendet werden.
In der Betrachtungsperiode sind insgesamt 85.800 € an Kosten für die folgenden Produktmengen entstanden:
| Sorte | Stück | Doseninhalt | Konservierungszeit in Minuten |
| A | 12.000 | 250 | 12 |
| B | 9.000 | 250 | 18 |
| C | 8.000 | 500 | 12 |
| D | 10.000 | 500 | 18 |
Wie hoch sind die Kosten je Sorte und je Dose einer Sorte.
| Sorte | Stück | Doseninhalt | Konservierungszeit in Minuten | ÄZ | K | k | |
| A | 12.000 | 250 | 12 | 1,0 | 12.000 | 14.400 | 1,2 |
| B | 9.000 | 250 | 18 | 1,5 | 13.500 | 16.200 | 1,8 |
| C | 8.000 | 500 | 12 | 2,0 | 16.000 | 19.200 | 2,4 |
| D | 10.000 | 500 | 18 | 3,0 | 30.000 | 36.000 | 3,6 |
| 71.500 |
85.800 / 71.500 = 1,2
Die ÄZ ergibt sich aus der Multiplikation des Doseninhalts mit der Konservierungszeit. Um nicht zu große Äquivalenzziffern zu erhalten, wurden sämtliche ÄZ durch 3.000 dividiert.
| Menge | Sorte | ÄZ | VE | K | k |
| 12.000 | 250*12= 3.000 | 1,00 | 12.000 | 14.400 | 1,20 |
| 9.000 | 250*18= 4.500 | 1,50 | 13.500 | 16.200 | 1,80 |
| 8.000 | 500*12= 6.000 | 1,00 | 16.000 | 19.200 | 2,40 |
| 10.000 | 500*18= 9.000 | 3,00 | 30.000 | 36.000 | 3,60 |
| 71.500 | 85.800 |
Aufgaben
1. Aufgabe
Welche zwei Aussagen sind richtig?
a. Durch eine Division der Leistungsmenge mit der Äquivalenzzahl werden die
geforderten Rechnungseinheiten ermittelt.
b. Die Äquivalenzzahlen geben das Kostenverhältnis der einzelnen Erzeugnisse
zueinander an.
c. Die geforderte Rechnungseinheit wird durch ein Additionsverfahren der
Faktoren Menge und Äquivalenzziffer festgestellt.
d. Die Gesamtkosten des Betriebes werden durch die Summe der Rechnungs-
einheiten dividiert. Das Ergebnis sind die Kosten der Rechnungseinheit.
2. Aufgabe
In der Paper GmbH in Zülpich werden drei verschiedene Papiersorten hergestellt.
Die Selbstkosten betragen 22.320 EUR
Für die Produktion der drei Produktionsmenge sind Gesamtkosten von 746.865 EUR festgestellt worden.
Welche zwei Aussagen sind richtig?
a. Durch eine Division der Leistungsmenge mit der Äquivalenzzahl werden die
geforderten Rechnungseinheiten ermittelt.
b. Die Äquivalenzzahlen geben das Kostenverhältnis der einzelnen Erzeugnisse
zueinander an.
c. Die geforderte Rechnungseinheit wird durch ein Additionsverfahren der
Faktoren Menge und Äquivalenzziffer festgestellt.
d. Die Gesamtkosten des Betriebes werden durch die Summe der Rechnungs-
einheiten dividiert. Das Ergebnis sind die Kosten der Rechnungseinheit.
2. Aufgabe
In der Paper GmbH in Zülpich werden drei verschiedene Papiersorten hergestellt.
| Sorte | Menge in kg | Äquivalenzziffer | ||
| ASS | 4.200 | 0,8 | ||
| BASS | 6.200 | 1,0 | ||
| CASS | 3.800 | 1,4 |
Die Selbstkosten betragen 22.320 EUR
Ermitteln Sie die Selbstkosten nach der Äquivalenzziffernmethode.
3. Aufgabe
Die Controllingabteilung im Hause von WEKA-Glas GmbH in Gerolstein ermittelt die Produktionsmenge von drei Sorten:
| Produkt HAS | 7.500 Stück | |
| Produkt SASS | 9.500 Stück | |
| Produkt KLAS | 2.800 Stück |
Für die Produktion der drei Produktionsmenge sind Gesamtkosten von 746.865 EUR festgestellt worden.
Es entstanden für das Produkt HAS 25 % mehr Kosten als für das Produkt SASS und Produkt Klas 12 % weniger als Sorte SASS.
Ermitteln Sie nach der Äquivalenzziffernmethode die Stück-und Gemeinkosten der drei Produkte.
4. Aufgabe
| Artikel | Produktionsmenge | Äquivalenzziffer | Gewinnzuschlag | |||
| ASS | 80.000 Stück | 1,0 | 15% | |||
| BASS | 72.000 Stück | 1,2 | 10% | |||
| CASS | 64.000 Stück | 1,6 | 12% |
Die Selbstkosten betragen 3.225.600 EUR
Ermitteln Sie den Nettoverkaufspreis für alle drei Artikel pro Stück.
Lösungen:
1. Aufgabe
a) Falsche Aussage
Richtig wäre:
Durch eine Multiplikation der Leistungsmenge mit der Äquivalenzzahl werden
die geforderten Rechnungseinheiten ermittelt.
b) Richtige Aussage
c) Falsche Aussage
Die geforderten Rechnungseinheiten werden wie folgt ermittelt:
Menge mal Äquivalenzziffer
d) Richtige Aussage
2. Aufgabe
1. Ermittlung der Umrechnungszahl
a) Falsche Aussage
Richtig wäre:
Durch eine Multiplikation der Leistungsmenge mit der Äquivalenzzahl werden
die geforderten Rechnungseinheiten ermittelt.
b) Richtige Aussage
c) Falsche Aussage
Die geforderten Rechnungseinheiten werden wie folgt ermittelt:
Menge mal Äquivalenzziffer
d) Richtige Aussage
2. Aufgabe
1. Ermittlung der Umrechnungszahl
| ASS | 4.200 x 0,8 | = | 3.360 | |||||
| BASS | 6.200 x 1,0 | = | 6.200 | |||||
| CASS | 3.800 x 1,4 | = | 5.320 | |||||
|
|
||||||||
| = | Summe | 14.880 | ||||||
|
|
||||||||
2. Ermittlung der Selbstkosten pro kg Papier
| Gesamtkosten | 22.320 | |||||
|
|
|
= | 1,50 EUR pro kg | |||
| Stückmenge | 14.800 |
| Sorte | Umrechnungszahl | Selbstkosten EUR | Selbstkosten pro kg EUR | |||
| ASS | 3.360 | 5.040 | 1,20 | |||
| BASS | 6.200 | 9.300 | 1,50 | |||
| CASS | 5.320 | 7.980 | 2,10 | |||
|
|
||||||
| Summe | 14.880 | 22.320 | ||||
3. Aufgabe
Feststellung der Äquivalenzziffern
HAS = 1,25, gegenüber SASS 25 % mehr
SASS = 1,0 SASS = 100 %
KLAS 0,88 gegenüber SASS 12 % weniger
| Sorten | Stück | Äquivalenzziffer | Menge |
|
Stückkosten in EUR |
|
Gesamtkosten in EUR | |||
| HAS | 7.500 | 1,25 | 9.375 | 43,75 |
|
328.12 | ||||
| SASS | 9.500 | 1,00 | 9.500 | 35,00 | 332.500 | |||||
| KLAS | 2.800 | 0,88 | 2.464 | 30,80 | 86.240 | |||||
|
|
|
|||||||||
| 21.339 | 746.865 |
Rechenschritte:
Menge
7.500 x 1,25 = 9.375
9.500 x 1,00 = 9.500
2.800 x 0,88 = 2.464
Gesamtkosten
746.865 : 21.339 x 9.375 = 328.125 EUR
746.865 : 21.339 x 2.464 = 86.230 EUR
746.865 : 21.339 x 9.500 = 332.500 EUR
Stückkosten
328.125 : 7.500 = 43,75 EUR
332.500 : 9.500 = 35,00 EUR
86.240 : 2.800 = 30,80 EUR
4. Aufgabe
| Artikel | Umrechnungszahl | Stückkosten der Sorte | Gewinn | Nettoverkaufspreis | ||||
| ASS | 80.000 | 12,00 | 1,80 | 13,80 | ||||
| BASS | 86.400 | 14,40 | 1,44 | 15,84 | ||||
| CASS | 102.400 | 19,20 | 2,30 | 21,50 | ||||
|
|
||||||||
| 268.800 |
|
letzte Änderung Günther Wittwer, Dipl. Volkswirt Friedrich Schnepf am 11.08.2024 |
Bleiben Sie auf dem Laufenden mit unserem Newsletter
Tragen Sie sich für den kostenfreien und unverbindlichen Newsletter von Controlling-Portal.de ein und erhalten Sie jeden Monat aktuelle Neuigkeiten für Controller. Wir informieren Sie über neue Fachartikel, über wichtige News, aktuelle Stellenangebote, interessante Tagungen und Seminare. Wir empfehlen Ihnen spannende Bücher und geben Ihnen nützliche Excel-Tipps. Verpassen Sie nie mehr wichtige Diskussionen im Forum und stöbern Sie in Software-Angeboten, die Ihnen den Arbeitsalltag erleichtern. Beispiel-Newsletter >>Jetzt Newsletter gratis erhalten
Premium-Stellenanzeigen
Medizinische Einrichtungen des Bezirks Oberpfalz – medbo KU
Regensburg
Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH
Ulm
INDUS Holding AG
Bergisch Gladbach bei Köln
Fraunhofer-Institut für Windenergiesysteme IWES
Bremerhaven
Eigenen Fachbeitrag veröffentlichen?
Sie sind Autor einer Fachpublikation oder Entwickler einer Excel-Vorlage? Gern können Sie sich an der Gestaltung der Inhalte unserer Fachportale beteiligen! Wir bieten die Möglichkeit Ihre Fachpublikation (Fachbeitrag, eBook, Diplomarbeit, Checkliste, Studie, Berichtsvorlage ...) bzw. Excel-Vorlage auf unseren Fachportalen zu veröffentlichen bzw. ggf. auch zu vermarkten. Mehr Infos >>Kommentar zum Fachbeitrag abgeben
Nur registrierte Benutzer können Kommentare posten!
- Die meist gelesenen Fachbeiträge
- Die neuesten Fachbeiträge
- Premium-Artikel
- Wissenstests
- Fachbeitrag einstellen
- Fachinfo-Kategorien
- Grundlagen (95)
- Branchen (49)
- Funktional (91)
- Kostenmanagement (30)
- Konzepte (84)
- Kennzahlen (373)
- Finanzplanung (63)
- Budgetierung (10)
- Reporting / Berichtswesen (35)
- BSC (7)
- Projektcontrolling (17)
- Kostenrechnung (414)
- IAS / IFRS (4)
- Risikomanagement (37)
- Investitionsrechnung (75)
- Unternehmensbewertg. (12)
- Rating (6)
- Business Intelligence (82)
- Excel-Tipps (202)
- Studien (8)
- Arbeitsmarkt (21)
- Spar-Tipps (2)
- Controlling-Journal (23)
- Finanzmathem. Formeln (15)
- Neulich im Golfclub (57)
- Softskills (29)
- Sonstiges (19)
- Artikel-Serien
- Stichwortverzeichnis
Controlling- Newsletter
Neben aktuellen Fach- und Arbeitsmarkt-Trends für Controller und neu eingegangene Fachbeiträge, informieren wir Sie über interessante Veranstaltungen und stellen Ihnen einzelne Controlling-Tools im Detail vor.Werden Sie jetzt monatlich über neue Fachbeiträge, Jobs und Tools informiert!
Zur Newsletter-Anmeldung >>
Über 3.000 Artikel und Vorlagen

Werden Sie Mitglied in einer großen Controller-Community (über 12.000 Mitglieder!) und erhalten Zugriff auf viele Inhalte und diskutieren ihre Fragen im Controlling-Forum.
Sehen Sie hier die neuesten Fachbeiträge >>
Eine neue Stelle?
Mit dem Studium fertig, Umzug in eine andere Region, Aufstiegschancen nutzen oder einfach nur ein Tapetenwechsel? Dann finden Sie hier viele aktuell offene Stellen im Controlling.Zu den Stellenanzeigen >>

Sie suchen einen Controller? Mit einer Stellenanzeige auf Controlling-Portal.de erreichen Sie viele Fachkräfte. weitere Informationen >>
KLR-Begriffe von A bis Z
Testen Sie ihr Wissen mit unseren Aufgaben und Lösungen im Bereich Kostenrechnung >>Sie haben eine Frage?

Nutzen Sie kostenfrei das Forum für Controller und und diskutieren ihre Fragen zu Controlling-Themen.
Riesen- Ressource
Auf Controlling-Portal.de sind bereits über 1.800 Fachbeiträge veröffentlicht und ständig kommen neue dazu.Zu den neuesten Fachbeiträgen >>
Zu den derzeit meistgelesenen Fachbeiträgen >>
Zu den Premium-Beiträgen >>
Sie möchten auch einen Fachbeitrag hier veröffentlichen? Dann erhalten Sie hier weitere Informationen >>
Neueste Excel-Vorlagen
Amüsante Glosse

Erfolgreiche Unternehmer einer Kleinstadt treffen sich regelmäßig im örtlichen Golfclub und diskutieren mit Ihrer Lieblingskellnerin und BWL-Studentin Pauline betriebswirtschaftliche Probleme. Amüsant und mit aktuellem Bezug geschrieben von Prof. Peter Hoberg.
Zur Serie "Neulich im Golfclub" >>
News
Sie möchten sich weiterbilden?

In unserer Seminar-Rubrik haben wir einige aktuelle Seminar- und Kurs-Angebote für Controller, u.a. auch Kurse zum Controller / IHK zusammengestellt.
Talentpool - Jobwechsel einfach!

Tragen Sie sich kostenfrei im Talentpool auf Controlling-Portal.de ein und erhalten Jobangebote und Unterstützung beim Jobwechsel durch qualifizierte Personalagenturen.
Excel. Aber in schnell

Beschleunigen Sie Ihr Reporting: Wie Sie Excel weiterhin nutzen – aber mit AnaplanXL effizienter, konsistenter und ohne manuelle Schleifen.
Jetzt anmelden, es gibt noch freie Plätze!
Stellenanzeigen
Sachbearbeitung externes Rechnungswesen (w/m/d) Die Bundesanstalt für Immobilienaufgaben (BImA) ist das Immobilienunternehmen des Bundes, das die immobilienpolitischen Ziele der Bundesregierung unterstützt und für fast alle Bundesbehörden die notwendigen Flächen und Gebäude zur Verfügung stellt. Dementsprechend sind wir in ganz Deutsch... Mehr Infos >>
Die Bundesanstalt für Immobilienaufgaben (BImA) ist das Immobilienunternehmen des Bundes, das die immobilienpolitischen Ziele der Bundesregierung unterstützt und für fast alle Bundesbehörden die notwendigen Flächen und Gebäude zur Verfügung stellt. Dementsprechend sind wir in ganz Deutsch... Mehr Infos >>
Controller*in für die Kosten- und Leistungsrechnung (KLR)
 Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
Teamleitung Betriebskosten (m/w/d)
 Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Teamleitung Finanzbuchhaltung (m/w/d)
 Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Mitarbeiter im Controlling/Financial Analyst (m/w/d)
 Die WIRTGEN GROUP ist ein international führender Unternehmensverbund der Baumaschinenindustrie mit rund 9.000 Beschäftigten weltweit. Als starker Teil von John Deere und mit unseren spezialisierten Marken WIRTGEN, VÖGELE, HAMM, KLEEMANN, BENNINGHOVEN, CIBER sowie Werken in Deutschland, Brasilien... Mehr Infos >>
Die WIRTGEN GROUP ist ein international führender Unternehmensverbund der Baumaschinenindustrie mit rund 9.000 Beschäftigten weltweit. Als starker Teil von John Deere und mit unseren spezialisierten Marken WIRTGEN, VÖGELE, HAMM, KLEEMANN, BENNINGHOVEN, CIBER sowie Werken in Deutschland, Brasilien... Mehr Infos >>
Controller mit Schwerpunkt Produkt-Kalkulation (m/w/d) in Vollzeit
 Wir, die Gubor-Gruppe, gehören als erfolgreiches, familiengeführtes Unternehmen mit rund 1.500 Mitarbeitern europaweit zu den Marktführern von Süßwarenartikeln. Unsere Produkte fertigen wir an fünf Standorten in Deutschland sowie einem Standort in Polen. Dabei setzen wir sowohl in der Beschaffung... Mehr Infos >>
Wir, die Gubor-Gruppe, gehören als erfolgreiches, familiengeführtes Unternehmen mit rund 1.500 Mitarbeitern europaweit zu den Marktführern von Süßwarenartikeln. Unsere Produkte fertigen wir an fünf Standorten in Deutschland sowie einem Standort in Polen. Dabei setzen wir sowohl in der Beschaffung... Mehr Infos >>
Controller*in für Institutsfinanzierungen
 Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geiste... Mehr Infos >>
Teamleitung Rechnungswesen (m/w/d)
 Im Auftrag unseres Kunden suchen wir eine Teamleitung Rechnungswesen (m/w/d) für ein mittelständisches IT-Beratungsunternehmen. Das Beratungsunternehmen umfasst sechs Geschäftsbereiche und beschäftigt insgesamt rund 145 Mitarbeitende. Der Hauptsitz liegt in Sachsen, ergänzt durch weitere ... Mehr Infos >>
Im Auftrag unseres Kunden suchen wir eine Teamleitung Rechnungswesen (m/w/d) für ein mittelständisches IT-Beratungsunternehmen. Das Beratungsunternehmen umfasst sechs Geschäftsbereiche und beschäftigt insgesamt rund 145 Mitarbeitende. Der Hauptsitz liegt in Sachsen, ergänzt durch weitere ... Mehr Infos >>
Weitere Stellenanzeigen im Stellenmarkt >>
Veranstaltungs-Tipp

Sie sind Controller und wollen Ihre Excel oder Power-BI Kenntnisse verbessern? Dann sind unsere Excel /Power-BI Schulungen genau das Richtige für Sie! Lernen Sie, wie Sie Daten effizient analysieren, visualisieren und präsentieren können. Nutzen Sie die Vorteile von Pivot-Tabellen, Formeln, Makros und mehr. Melden Sie sich jetzt an und werden Sie zum Excel oder Power-BI Profi!
Mehr Infos >>
JOB- Letter

Sie möchten über neu eingehende Stellenangebote automatisch informiert werden? Dann können Sie unseren kostenfreien Jobletter abonnieren. Mit diesem erhalten Sie alle 14 Tage die aktuellsten Stellenanzeigen und weitere Arbeitsmarkt-News.
Excel-Tool Plankostenrechnung
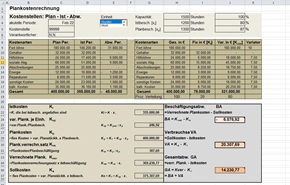
Nach Eingabe der Plankosten und Ist-Kosten für eine Kostenstelle und Periode, sowie der Aufteilung der Kosten in variable und fixe Kosten, werden formelgestützt alle relevanten Größen (Sollkosten, verrechnete Plankosten etc.) ermittelt und eine Abweichungsanalyse (rechnerisch und grafisch) durchgeführt.
Jetzt hier für 25,- EUR downloaden >>
Excel-Tools für Controller!

Über 500 Vorlagen direkt zum Download. Verschaffen Sie sich einen Überblick >>
Software-Tipps

Der BusinessPlanner besticht seit Jahren durch seine schnelle und professionelle Umsetzung einer integrierten Unternehmensplanung. Ein besonderer Fokus liegt auf der Integration von Planbilanz und Finanzplan / Cashflow – inklusive transparentem und aussagekräftigem Reporting.
Mehr Informationen >>

LucaNet.Planner deckt alle Anforderungen der integrierten Unternehmensplanung, des Reportings und der Analyse ab. Setzen Sie auf eine Software, die Ihnen mit maximaler Transparenz Arbeitsprozesse erleichtert. Mit wenigen Mausklicks passen Sie vorgefertigte Strukturen an Ihre Bedürfnisse an und importieren Ist-Zahlen über fertige Schnittstellen aus Ihrem Vorsystem. Mehr Informationen >>

Die IDL CPM Suite ist eine Software für die Unternehmenssteuerung mit integrierten Applikationen für Konzernkonsolidierung, Finanzplanung, operative Planung, Managementreporting, regulatorisches Berichtswesen und Analyse. Herausragende Usability, hohe Automatisierung und Fachlichkeit zeichnen sie aus. Mehr Informationen >>
Weitere Controlling-Software-Lösungen im Marktplatz >>
Kreditrechner - 50 Darlehen in Excel verwalten

Mit diesem Kreditrechner für Excel hast du deine gesamte Schuldenlage im Griff – einfach, übersichtlich und effektiv. Spare bares Geld durch bessere Planung. Dieser Planer wurde speziell dafür entwickelt, auch bei komplexen Kreditstrukturen Übersicht und Kontrolle zu behalten. Bis zu 50 Kredite gleichzeitig verwalten und Laufzeiten bis zu 50 Jahre abbilden
Jetzt hier für 17,90 EUR downloaden!
E-Book Controlling-Instrumente
Der erfahrene Controller und Excel-Coach Kristoffer Ditz stellt in seinem E-Book "Controlling-Instrumente" mit ebenso einfachen wie hilfreichen Tools für alle Controller-Lebenslagen vor. Preis 8,90 EUR hier bestellen >> Excel TOP-SellerRS Liquiditätsplanung L
Die RS Liquiditätsplanung L ist ein in Excel erstelltes Werkzeug für die Liquiditätsplanung von Kleinunternehmen sowie Freiberuflern. Die Planung erfolgt auf Basis von veränderbaren Einnahmen- und Ausgabepositionen. Detailplanungen können auf extra Tabellenblättern für z.B. einzelne Projekte oder Produkte vorgenommen werden.
Mehr Informationen >>
Rollierende Liquiditätsplanung auf Wochenbasis
Dieses Excel-Tool bietet Ihnen die Grundlage für ein Frühwarnsystem. Der erstellte Liquiditätsplan warnt Sie vor bevorstehenden Zahlungsengpässen, so dass Sie frühzeitig individuelle Maßnahmen zur Liquiditätssicherung einleiten können. Gerade in Krisensituationen ist eine kurzfristige Aktualisierung und damit schnelle Handlungsfähigkeit überlebenswichtig. Mehr Informationen >>Strategie-Toolbox mit verschiedenen Excel-Vorlagen
Die Strategie-Toolbox enthält 10 nützliche Excel Vorlagen, die sich erfolgreich in der Strategie bewährt haben. Alle Tools sind sofort einsatzbereit und sind ohne Blattschutz. Damit können die Vorlagen individuell angepasst werden. Ideal für Mitarbeiter aus dem strategischen Management. Mehr Informationen>>
Weitere über 400 Excel-Vorlagen finden Sie hier >>
Software-Tipp
 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>  RS Controlling-System: Das RS- Controlling-System bietet Planung, Ist- Auswertung und Forecasting in einem Excel-System. Monatliche und mehrjährige Planung. Ganz einfach Ist- Zahlen mit Hilfe von Plan/Ist-Vergleichen, Kennzahlen und Kapitalflussrechnung analysieren.
RS Controlling-System: Das RS- Controlling-System bietet Planung, Ist- Auswertung und Forecasting in einem Excel-System. Monatliche und mehrjährige Planung. Ganz einfach Ist- Zahlen mit Hilfe von Plan/Ist-Vergleichen, Kennzahlen und Kapitalflussrechnung analysieren. 





