Fehlinterpretationen in Excel-Tabellen im Reporting

Dieser Artikel ist der vierte Artikel einer Reihe von Beiträgen, die sich mit bewussten oder unbewussten Manipulationen an grafischen Darstellungen, Tabellen und Rechenergebnissen befasst und deren Auswirkungen auf die Interpretation des Dargestellten und die Konsequenzen für darauf basierende Schlussfolgerungen und Entscheidungen aufzeigt.

In dem folgenden Beitrag geht es darum, inwiefern die Anwendung des Programms Microsoft Excel (kurz: Excel) zu Fehlinterpretationen von Zahlenergebnissen, auch von Kennzahlen, führen kann.

Nicht nur im Controlling wird Excel gerne genutzt, um manuell eingegebene oder aus anderen Programmen übertragene Zahlen in Tabellenform darzustellen, die in Excel integrierten Formeln zur Berechnung von Kennzahlen anzuwenden und/oder grafische Darstellungen aus Excel heraus zu erstellen.

Der Vorteil gegenüber einer manuellen Ermittlung von Rechenergebnissen mit dem Taschenrechner liegt auf der Hand. Auch die von Excel zur Verfügung gestellten "selbst rechnenden" Formeln sind bei der Verarbeitung größerer Datenmengen praktisch, wenn auch nicht immer ganz leicht anwendbar. Darin liegt auch gleichzeitig die Gefahr für eine mögliche Fehl-Interpretation, da die Berechnungsmethoden, die hinter den Formeln stehen, sowohl von der Anwenderin als auch vom Betrachter des Ergebnisses richtig verstanden werden müssen, damit die jeweils passende Formel für jeden Anwendungsfall ausgewählt wird, die passenden Daten zur Berechnung eingegeben werden und das Ergebnis dann auch dazu passend interpretiert wird.

Selbst die in einer simplen Excel-Tabelle "versteckten" Formeln wie die Summenformel oder eine Prozentberechnung sind nur sichtbar, wenn man die Excel-Tabelle als Excel-Tabelle vorliegen hat und nicht in einem Ausdruck oder einem Screenshot. Und wie die im Folgenden geschilderten Beispiele verdeutlichen, "steckt nicht immer das drin, was draufsteht" oder was erwartet wird. Die Ergebnisse werden entsprechend der eigenen Erwartung interpretiert und nicht entsprechend dem, was sie tatsächlich aussagen. Wenn dann eine Tabelle erst einmal Einlass in das regelmäßige Reporting gefunden hat, wird meist nicht mehr überprüft, ob die Tabelle auch das zeigt, was sie vorgibt zu zeigen. Erst wenn Ergebnisse durch eine Veränderung der Grundsituation plötzlich offensichtlich unplausibel werden, gibt dies Anlass zum Überprüfen.

Im Folgenden werden zur Verdeutlichung des Problems folgende Beispielfälle vorgeführt.

1. Der Inhalt eines Excelfelds entspricht nicht der Erwartung.
2. Die verwendete Excel-Formel passt nicht zum Anwendungsfall, wird falsch angewendet oder das Ergebnis wird falsch interpretiert, weil die Berechnungsmethodik nicht bekannt ist

Zu 1. Inhalt eines Excelfelds entspricht nicht der Erwartung

Die vermutlich einfachste Rechenoperation in Excel ist die Summe über mehrere Zahlenwerte, die meist oberhalb oder links von dem Summenfeld aufgelistet sind. Da dieses Summenfeld typischerweise in fast jeder Tabelle vorkommt, interpretiert man ein einzelnes Feld am Ende einer Liste, das einen deutlich höheren Wert enthält, als die Einzelwerte in der Liste, automatisch als Summe dieser Einzelwerte.

Das folgende Bespiel könnte konstruiert wirken, ist aber ein reales Beispiel aus der Praxis. Schauen Sie sich die folgende Zahlenreihe, die einem professionellen Businessplan entstammt, einmal genau an [1].

	3. Quartal			4. Quartal			Geschäftsjahr
	Jul	Aug	Sep	Okt	Nov	Dez	Jun – Dez
Umsatzerlöse	38.804	39.325	50.700	53.236	55.897	58.692	379.542

Wie gesagt, würde man normalerweise erwarten, dass die Zahl ganz rechts für das Geschäftsjahr die Summe der sechs Zahlen links davon darstellt. Wenn man genauer hinschaut, sieht man aber, dass in der "Summe" das gesamte Gründungsjahr abgebildet ist, das aber offenbar bereits im Juni beginnt, während die Zahlen links davon erst mit dem Monat Juli starten. Die Differenz zwischen der Summe der sechs Werte (379.542) und der Summe der abgebildeten Einzelwerte beträgt 82.888. Inhaltlich müsste das also der fehlende Juni-Wert sein.

Tatsächlich gibt es hier aber eine weitere Unstimmigkeit, da die Werte von Juli bis Dezember stetig ansteigen, was für eine Existenzgründung auch Sinn ergibt. Der fiktive Juni-Wert liegt damit deutlich über dem Wert, der vermutlich tatsächlich in der Planung vorgesehen war.

Ob es sich hier um eine bewusste Manipulation handelt, soll nicht diskutiert werden. Wie eine solche zu Fehl-Interpretationen verleitende Darstellung aber entstehen kann, ist ganz einfach erklärt. Abgesehen davon, dass es sehr unglücklich ist, den Juni nicht als Wert gesondert darzustellen, wurde hier möglicherweise die Tabelle aus Excel heraus in Word kopiert und anschließend wurden einzelne Werte verändert, ohne daran zu denken, dass sich die Summe in Word natürlich nicht mehr automatisch mit verändert.

Die Wirkung ist fatal: Da man nicht damit rechnet, dass der Gesamtwert nicht die korrekte Summe enthält, könnte jemand, der die Existenzgründung beurteilen soll und die einzelnen Werte für plausibel und womöglich auch für erreichbar erachtet, damit automatisch auch den Wert für das gesamte Jahr "abnicken", obwohl dieser sicher um mehr als 10 % zu hoch angesetzt ist, wenn der Juni-Wert eher bei 30.000 als bei 80.000 liegt.

Ein solcher Übertragungsfehler kann auch innerhalb von Excel auftreten, wenn eine Tabelle ohne die dahinterliegenden Formeln kopiert wird, also nur die Zahlenwerte übernommen werden. Das kann man in Excel auswählen, wenn man von den in der folgenden Abbildung dargestellten Einfügeoptionen die 2. Option, die mit den Ziffern 123, wählt.



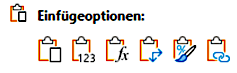
Diese Vorgehensweise kann Sinn ergeben, wenn sich die Formeln der Ursprungstabelle auf andere Felder oder andere Tabellen beziehen und man diesen Bezug nicht in die neue Tabelle übernehmen möchte. Dadurch verschwinden aber alle Formeln, auch die, die vielleicht weiterhin sinnvoll wären, wie z. B. eine Summenformel oder eine Prozentangabe. Ändert man dann Zahlenwerte in der neuen Tabelle, passt sich der Summenwert oder Prozentwert nicht an und es entsteht ein ähnliches Problem wie oben geschildert.

Beispiel: Der Wert 1150 im Feld B5 der folgenden Tabelle könnte die Summe der Kosten für einen Bereich beinhalten, dessen prozentuale Aufteilung auf vier Kostenarten in Spalte C zu sehen ist.

A	B	C
1	100	9 %
2	300	26 %
3	250	22 %
4	500	43 %
5	1150	100 %

Rechnet man nun mit einer 10 %-igen Erhöhung der Kostensumme von 1150 auf 1265 und möchte wissen, wie sich diese neue Summe auf die vier Kostenarten verteilen wird, sofern sich die prozentuale Aufteilung nicht verändert, so kann man z. B. wie folgt vorgehen: Man errechnet die Kostenwerte in Spalte D, indem man auf die Prozentwerte in Spalte C zurückgreift und diese mit dem Wert 1265 verknüpft. Kopiert man dann noch die Spalte C in Spalte E – inklusive der Formeln zur Berechnung des Prozentwertes – dann ist "alles richtig".

A	B	C	D	E
1	100	9 %	=C1*D5=114	=D1/D5=9%
2	300	26 %	=C2*D5=329	=D2/D5=26%
3	250	22 %	=C3*D5=278	=D3/D5=22%
4	500	43 %	=C4*D5=544	=D4/D5=43%
5	1265	100 %	1265	=D5/D5=100%

Werden dann nachträglich die Werte in Spalte D verändert, rechnet Excel die neuen prozentualen Anteile korrekt aus, z. B. so:

A	B	C
1	150	12 %
2	293	23 %
3	278	22 %
4	544	43 %
5	1265	100 %

Tippt man aber die prozentualen Anteile, die man übertragen will, manuell als Zahlenwerte und nicht als Formeln in die Spalte E ein und berechnet die Werte in Spalte D, indem man den jeweiligen Prozentwert mit dem Wert 1265 verknüpft, dann erhält man zwar zunächst das gleiche Ergebnis.

Wenn dann aber an den Zahlenwerten in Spalte D etwas geändert wird, passen sich die Prozentwerte in Spalte E nicht automatisch an, da sie ja fix als Zahlenwerte eingegeben wurden. Die folgende Tabelle zeigt ein solches mögliches Ergebnis, bei dem man – und das ist hier der Punkt - nicht zwangsläufig sofort erkennt, dass die Prozentanteile in Spalte E nicht mehr zu der Aufteilung der Zahlen in Spalte D passen:

A	B	C
1	150	9 %
2	293	26 %
3	278	22 %
4	544	43 %
5	1265	100 %

Auffallen würde dies erfahrungsgemäß erst dann, wenn die Prozentwerte so unplausibel werden, dass der Fehler offensichtlich wird.

Zu 2. Fehlerhafte Anwendung oder Interpretation einer Excel-Formel

Excel stellt eine Vielzahl an Formeln zur Berechnung verschiedener Kennzahlen zur Verfügung, u.a. aus der Finanzmathematik. Dabei lohnt sich die Anwendung dieser Formeln besonders dann, wenn man eine große Menge an Daten zu verarbeiten hat oder die Rechenmethodik selbst relativ kompliziert ist. Problematisch ist dabei, dass es die Anwender:innen nicht der Verantwortung enthebt, selbst genau zu wissen, "was Excel da tut". Wird eine Formel dann inhaltlich falsch interpretiert oder es werden falsche Daten eingegeben, führt dies automatisch zu einer Fehlinterpretation des Ergebnisses.

Das folgende Beispiel demonstriert die Problematik anhand des Kapitalwerts. Die Definition des Kapitalwerts C lautet üblicherweise wie folgt:



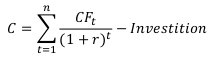
Eine Reihe von n Cashflows (CF_t) wird auf den Zeitpunkt t=0 mit dem Zins r abgezinst; anschließend werden die abgezinsten Cashflows zusammenaddiert und von dieser Summe die Investitionssumme abgezogen. In dieser Definition wird davon ausgegangen, dass die Zeitpunkte t=1, …, n alle gleich weit voneinander entfernt sind (üblicherweise ein Jahr).

Hält man nun in Excel unter den angebotenen Formeln nach einer geeigneten Berechnungshilfe Ausschau, findet man u.a. die folgenden:

• XKAPITALWERT, 
• BW (Barwert) und 
• NBW (Nettobarwert). 

Es liegt aufgrund des Namens nahe, sich als erstes mit XKAPITALWERT zu beschäftigen. Die Formel lässt sich auch tatsächlich zur Berechnung eines Kapitalwertes verwenden, allerdings entspricht der Inhalt nicht der üblichen o. a. Definition, da die Excel-Formel auch unterschiedliche Zeitabstände zwischen den erfassten Cashflows zulässt. Daher muss man bei Anwendung der Formel nicht nur die Werte der Cashflows eingeben, sondern auch Datumsangaben für den Zeitpunkt des Eintretens jedes einzelnen Cashflows. Wenn wie in der o. a. Definition immer Ein-Jahresabstände zwischen den Cashflows vorliegen, ist die Excel-Formel also unnötig kompliziert.

Ein Zahlenbeispiel: Angenommen t=0 sei das Jahr 2023, die Investition soll am 1.1.2023 erfolgen und alle weiteren Cashflows (s. folgende Tabelle) treten immer genau ein Jahr später auf, also immer am 1.1. des jeweiligen Folgejahres. Der Zinssatz soll 6% betragen. Die folgenden Werte sind in diese Excel-Formel einzutragen:

=XKAPITALWERT(Zins;Werte;Zeitpkte)

möglichst durch Markieren der entsprechenden Zeilen und nicht durch Eintippen der einzelnen Zahlen.

CF Werte	-1.000	100	200	500	1.000
Zeitpunkte	1.1.2023	1.1.2024	1.1.2025	1.1.2026	1.1.2027

Excel errechnet daraus einen Kapitalwert von 484,02. Rechnet man dagegen den Kapitalwert nach der o. a. Definition wie folgt manuell aus, erhält man den Wert 484,24.

100	+	200	+	500	+	1.000	-	1.000	=	484,24
1,06		(1,06)2		(1,06)3		(1,06)4

Obwohl man zu Recht identische Ergebnisse erwarten könnte, weichen die beiden Werte – wenn auch nur geringfügig – voneinander ab. Vermutlich liegt das daran, dass es bei n>3 immer mindestens ein Schaltjahr gibt, das von Excel dann mit 366 Tagen anstelle von sonst 365 Tagen berücksichtigt wird.
Als passgenauer für die übliche Berechnung des Kapitalwertes stellt sich die Formel NBW (Nettobarwert) heraus. Hier wird automatisch von immer gleichen Ein-Jahres-Zeiträumen ausgegangen. Allerdings bezieht die Formel die Investitionssumme von -1000 nicht mit ein, sondern der Wert muss anschließend noch von dem ermittelten NBW abgezogen werden. Gibt man also in die Excel-Formel =NBW(Zins;Wert1;Wert2;…) Folgendes ein: =NBW(0,06;100;200;500;1.000), erhält man den Wert 1484,24.

Von diesem Wert ist die Investitionssumme abzuziehen, damit erhält man exakt den Wert von 484,24, der sich auch nach der Anwendung der ursprünglichen Definition ergibt. Interpretiert man die Angaben "Wert1;Wert2;…" dagegen falsch und gibt daher versehentlich Folgendes ein: =NBW(0,06;-1.000;100;200;500;1.000),

weil man annimmt, dass der Wert 1 die Investitionssumme darstellen soll, dann erhält man das Ergebnis 456,83, weil die Abzinsung "verschoben" ist: Schon die Investitionssumme wird mit t=1 abgezinst, der Wert 100 mit t=2 statt mit t=1 usw.. Trotzdem ist das Ergebnis nicht so weit von dem korrekten Wert entfernt, dass es allen sofort auffallen würde – nur, wenn man das Ergebnis manuell nachprüft – aber dass das nicht passiert, ist ja genau das Problem; man vertraut der Formel und dem:r Anwender:in.

Auch die Formel =BW (Barwert) scheint eine geeignete Formel für den Kapitalwert zu enthalten, denn der Kapitalwert ist ja nichts anderes als ein Barwert. Tatsächlich werden aber hier Annuitäten berechnet und die Formel eignet sich daher nicht zur Anwendung für die übliche Definition des Kapitalwertes.

Zusammenfassung

Das Tabellenkalkulations-Programm Microsoft Excel bietet eine Reihe von Unterstützungen bei der Erstellung von Tabellen und bei der Berechnung von Kennzahlen. Dabei können Zahlenwerte als Zahlen eingetragen werden oder auch durch Verknüpfung mit anderen Tabellen(-feldern) oder durch Eingabe von Formeln. Sowohl die fixe Eingabe von Zahlenwerten in Feldern, in denen ursprünglich eine Formel stand, als auch das Kopieren von "verformelten" Feldern, bei denen dann der Bezug zu anderen Tabellenfeldern nicht mehr stimmt, können zu falschen Ergebnissen führen, die aber von Betrachter:innen der Tabellen möglicherweise nicht erkannt werden (können).

Will man die von Excel zur Verfügung gestellten Formeln korrekt anwenden, ist es nötig, sich damit auseinanderzusetzen, welche Formel für welchen Anwendungsfall geeignet ist, welche Daten wie eingegeben werden müssen und wie das Ergebnis dann korrekt zu interpretieren ist. Wendet man Formeln an, die eine andere Definition einer Kennzahl beinhalten, als die übliche (bewusst oder unbewusst), so muss man damit rechnen, dass die Empfänger der Ergebnisse dies nicht bemerken und die Ergebnisse daher falsch interpretieren.



Fußnote:

[1] Zahlen wurden aus Geheimhaltungsgründen abgewandelt, ohne die inhaltliche Aussage dadurch zu verändern

letzte Änderung P.D.U.B. am 09.01.2023 Autor:  Dr. Ursula Binder

Autor:in

Frau Prof. Dr. Ursula Binder Professorin für Betriebswirtschaftslehre, insbesondere Rechnungswesen und Controlling an der TH Köln, vorher kaufmännische Leiterin eines mittelständischen Dienstleistungsunternehmens, Unternehmensberaterin, Seminarleiterin (Inhouse und öffentliche Seminare), Verfasserin von Lernbriefen für das Fernstudium, Autorin: Nachhaltigkeitsberichterstattung in mittelständischen Unternehmen, Haufe 2024, Schnelleinstieg Controlling, 8. Auflage 2023, Die 5 wichtigsten Steuerungsinstrumente für kleine Unternehmen, 1. Auflage 2017, Kennzahlen-Guide für Controller, 1. Auflage 2019.

weitere Fachbeiträge des Autors | Forenbeiträge