![Gross Margin Return on Investment (GMRoI): Aussagekraft und Probleme]()
Unternehmen analysieren mit vielen unterschiedlichen
Kennzahlen ihr Geschäft, immer auf der Suche nach Verbesserungsmöglichkeiten. So wird auch vorgeschlagen, die
Gross Profit Margin (kurz Gross Margin) auf das eingesetzte Kapital zu beziehen. Die resultierende Größe wird dann
Gross Margin Return on Investment (GMRoI) genannt. Teilweise wird noch ein I für Inventory angehängt, weil man sich auf den wertmäßigen durchschnittlichen
Lagerbestand als Investition konzentriert. Diese Variante gibt insbesondere für den Handel an, wie gut der Lagerbestand genutzt wird. Damit soll die Produktpolitik unterstützt werden.
Die Ermittlung des Gross Margin RoI stellt ein ehrgeiziges Unterfangen dar, weil eine Größe aus dem externen Rechnungswesen auf das eingesetzte Kapital bezogen wird. Bei der Vermischung von
Periodengrößen und
Kapitalgrößen kann es leicht Probleme geben, wenn die Größen nicht außerordentlich genau definiert werden.
1. Zusammensetzung GMRoI
Beim
Gross Profit werden vom
Nettoumsatz die
Cogs (Cost of goods sold) abgezogen. Der Gross Profit wird absolut und insbesondere auch als prozentualer Gross Profit, also prozentual in Bezug auf den Nettoumsatz, angegeben. Die Gross Profit Margin soll darüber informieren, wie viel vom Nettoumsatz verbleibt, wenn alle
produktions- und Supply Chain-bedingten Kosten abgezogen sind. Der Rest dient dann zur Abdeckung der Vertriebs-, Marketing-, R&D- und Verwaltungskosten. Das, was dann ggf. noch übrig bleibt, stellt den
Gewinn vor Kapitalkosten und Ertragssteuern dar.
Da die
Kapitalkosten in der Definition nicht enthalten sind, kann es sein, dass bestimmte
Geschäftsbereiche,
Produktgruppen oder auch
Produkte zwar gute Gross Margins aufweisen, aber so viel Kapital benötigen, dass sie aus Gesamtsicht nicht vorteilhaft für das Unternehmen sind. Daher wird die Gross Margin auf das eingesetzte Kapital bezogen, um so eine Art von
Kapitalrendite zu ermitteln. Es ist keine echte Rendite, weil insbesondere viele weitere Fixkostenanteile nicht berücksichtigt sind.
Häufig wird die GMRoI sogar nur auf den eingesetzten wertmäßigen
Lagerbestand eines Produktes oder einer Produktgruppe bezogen. Besonders im Handel versucht man damit herauszufinden, ob der Lagerbestand produktiv genug arbeitet. In diesem Fall fehlen dann alle anderen
Investitionen, für die dann weitere
Kapitalbeträge notwendig sind. Die Höhe der Investitionen ist nicht einfach zu bestimmen, weil die Bilanzansätze häufig nicht den
Marktwerten entsprechen.
Formelmäßig lautet die Definition des GMRoI wie folgt:
|
GMRoI =
|
GP / IK
|
|
|
|
|
GP
|
Gross Profit einer Periode in €/Pe
|
|
IK
|
Investiertes Kapital
|
Wenn der Gross Profit des Jahres 2020 beispielsweise 100 T€ betragen hat und das investierte Kapital 500 T€, so erhält man als Ergebnis eine Rendite von 20 %. Diese kann dann mit den Renditen anderer Produkte verglichen werden.
Das investierte Kapital IK besteht bei Anwendungen im Handel nur aus dem Wert des notwendigen Fertigwarenbestandes zur Aufrechterhaltung der
Lieferfähigkeit. Da nur ein Teil des Kapitals betrachtet wird, ist die Rendite dann wesentlich höher. Wenn dieses Kapital zum Beispiel 100 T€ beträgt, so ergibt sich die Rendite zu 100 %.
Für den Wert des investierten Kapitals ist meistens keine Zeitangabe angegeben. Man weiß somit nicht, ob es sich um den
Anfangsbestand, den
Durchschnitt oder einen anderen Bestand handelt. Dies wird weiter unten aus der
Renditedefinition abgeleitet. Die Gleichung GP/IK kann erweitert werden um den Nettoumsatz U
N. Dann erhält man:
GMRoI = (GP/ U
N) * (U
N / IK)
Die prozentuale
GP-Marge (erster Klammerausdruck) wird dann mit der
Lagerumschlagshäufigkeit (zweiter Klammerausdruck) multipliziert. Ein Produkt ist dann gut, wenn es eine gute Marge hat und gleichzeitig auch noch einen hohen Lagerumschlag aufweist. Ein bestimmter GMRoI kann somit mit unterschiedlichen Kombinationen von Marge und Lagerumschlagshäufigkeit erreicht werden.
In diesem Beitrag werden die unterschiedlichen Definitionen der verwendeten Größen mit ihren Problemen herausgearbeitet und dann ermittelt, welche Aussagekraft die Größe hat bzw. nicht hat. Es wird sich herausstellen, dass nur eng begrenzte Fragestellungen beantwortet werden können.
Anzeige
 Kennzahlen-Guide für Controller:
Kennzahlen-Guide für Controller:
Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT.
Taschenbuch Preis:19,90 Euro
Bei Amazon bestellen >>
2. Untersuchung der Größen
2.1. Gross Profit
Die Formel für den Gross Profit GP lautet wie folgt:
|
GP =
|
UN – KPSC in €/Pe
|
|
|
|
|
GP
|
Gross Profit in €/Pe
|
|
UN
|
Nettoumsatz in €/Pe
|
|
KPSC
|
Kosten der Produktion und Supply Chain (Cogs) in €/Pe
|
Auf den ersten Blick sehen die üblichen Definitionen einfach aus. Vom jeweiligen Nettoumsatz werden beim Gross Profit
alle produktionsbedingten Kosten abgezogen. Beide Größen sind immer auf eine bestimmte Periode bezogen. Es wird also etwa nach dem Gross Profit des Jahres 2022 gefragt. Daher muss für alle Geschäftsvorfälle entschieden werden, ob sie ganz oder teilweise in die fragliche Periode gehören. Es tauchen somit viele zeitliche Abgrenzungsprobleme auf, wobei sie umso schlimmer werden, je kürzer die Periode ist. Insbesondere die Behandlung selbst erstellter
immaterieller Vermögensgegenstände (Marke, Entwicklung, Lizenzen etc.) kann die Ergebnisse wesentlich beeinflussen.
Der Gross Profit wird in der Einheit
€ in der Mitte der betrachteten Periode (€/Pe) gemessen (vgl. hierzu Hoberg (2004); S. 271 ff.). Diese Zeitdefinition passt schlecht zu den Renditen, wie weiter unten zu zeigen sein wird.
Die
Kosten KPSC beinhalten auch alle
Fixkosten, welche in der
Produktion und in der
Supply Chain anfallen. Kosten in anderen Abteilungen werden nicht abgezogen, auch wenn sie variabel sind. Damit dürften eigentlich keine Entscheidungen auf der Basis von Gross Profits getroffen werden (vgl. hierzu Hoberg (2021), S. 1 ff.). In Abschnitt 3 wird ein entsprechendes Beispiel vorgestellt.
2.2 Kapitalrenditen
Im nächsten Schritt muss geklärt werden, wie Renditen beschaffen sind. Bei dem GMRoI handelt es sich um eine
Kapitalrendite (vgl. zur Abgrenzung zu den
Umsatzrenditen Hoberg (2016), S. 1029 ff.). Kapitalrenditen geben den durchschnittlichen
jährlichen Wertzuwachs an. Eine Investition mit einer Anfangsauszahlung von 1000 €
0, welche nach einem Jahr einen Rückfluss von 1100 €
1 erzeugt, weist einen Wertzuwachs von 10 % auf. Wichtig ist dabei die zeitliche Dimension. Es geht genau um ein Jahr.
Wenn die Investitionsdauer von diesem einen Jahr abweicht, muss der Wertzuwachs auf ein Jahr umgerechnet werden. Ausgangspunkt dabei ist die allgemeine
Aufzinsgleichung für einen Anfangsbetrag AB
0, der nach tn Jahren zu einem Endbetrag von EB
tn führt (vgl. z. B. Varnholt/Hoberg/Gerhards/Wilms, S. 81 ff.):
AB
0 * (1 + r)
tn = EB
tn
|
AB0
|
Anfangsbetrag in t=0, in €0
|
|
r
|
jährliche Rendite
|
|
tn
|
Anzahl Verzinsungsperiode (üblicherweise in Jahren)
|
|
EBtn
|
Endbetrag in t=tn, in €tn
|
Besonders schwierig kann es werden, wenn unterjährige Zahlungen vorliegen, zumal sie vom externen Analysten kaum abzuschätzen sind. Für interne Zwecke müssten
Zusatzauswertungen stattfinden, mit denen zu ermitteln ist, wann die Nettoumsätze zu Einzahlungen werden, und wann die Cogs (Cost of goods sold) zu Auszahlungen werden. Erst dann kann eine seriöse Kalkulation stattfinden.
Für den
Return on Investment (RoI) erfolgt fast immer eine
jährliche Betrachtung. Daraus folgt, dass modelltechnisch angenommen wird, dass eine Investition zu Beginn (t=0) vorgenommen wird, die nach einem Jahr, also in t=1, zu einer hoffentlich höheren Rückzahlung führt. Das Problem ist offensichtlich. Insbesondere die laufenden Ein- und Auszahlungen kommen nicht am Jahresanfang oder Jahresende, sondern verteilen sich auf das Jahr. Somit wird es notwendig werden, in einem vorbereitenden Schritt, die Zahlungen auf diese beiden Zeitpunkte zu transformieren.
Ansonsten kann es zu extrem unterschiedlichen Ergebnissen kommen, wie es die folgenden Beispiele aufzeigen. Dabei wird ein Lagerbestand von 200 € unterstellt. Der Einfachheit halber wird nur eine Periode betrachtet. Die Nettoumsätze mögen 200 € betragen und die Cogs 100 €. Es sei dabei nochmals betont, dass die Ermittlung des Gross Profit keine expliziten Annahmen trifft, wann die Nettoumsätze bzw. die Cogs im Laufe des Jahres anfallen. Der Gross Profit ergibt sich dann nach herkömmlicher Rechnung zu 100 €, was dann angesichts der Lagerinvestition von 200 €
0 zu 50 % GMRoI führt. Das ist aber nicht realistisch, was die folgenden Beispiele zeigen.
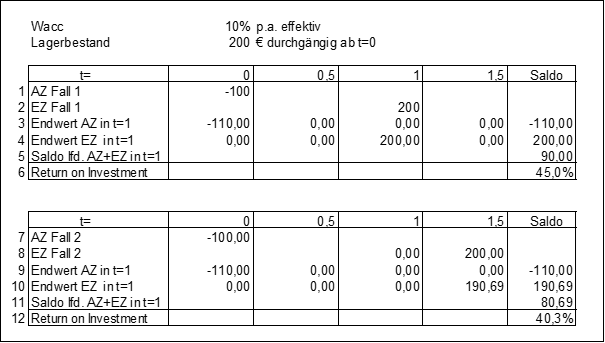 Abb. 1: Beispiele für GMRoIs
Abb. 1: Beispiele für GMRoIs
Nettoumsätze und Cogs müssen - wie oben gezeigt - erst einmal in Zahlungen zu den
Zeitpunkten t=0 und t=1 umgerechnet werden, damit überhaupt eine Kapitalrendite errechnet werden darf. Im vereinfachten Beispiel Teil 1 wird davon ausgegangen, dass die Einzahlungen - wenig realistisch - alle am Ende des ersten Jahres kommen. Für die laufenden Auszahlungen wird zunächst angenommen, dass sie gleich zu Jahresbeginn anfallen.
Eine Verrechnung der laufenden Zahlungen ist somit noch nicht statthaft, weil sie zu unterschiedlichen Zeitpunkten anfallen. Es müssen somit erst einmal intraperiodische Verzinsungen stattfinden (vgl. Varnholt / Hoberg / Gerhards / Wilms, S. 28 ff.). Da es sich um ein einfaches Beispiel handelt, ist die Anfangsinvestition in das Lager in Höhe von 200 €
0 bereits auf den Startzeitpunkt t=0 bezogen.
In der ersten Variante sind die laufenden Auszahlungen bereits in t=0 zu bezahlen (Zeile 1) und die Einzahlungen fließen in t=1 zu (Zeile 2), was sicherlich eine wesentliche Vereinfachung darstellt. Da die Rendite die Investition in t=0 erfordert, den Überschuss aber ein Jahr später, sollte die
laufende Auszahlung von -100 €0 auch auf t=1 hochgezinst werden, was dann -110 €
1 entspricht (Zeile 3). Da die Zahlungen jetzt zeitlich exakt verrechnet werden, kann mit dem
Zeitindex t in den Einheiten genau dokumentiert werden, wann die Zahlungen wirksam werden (vgl. Hoberg (2018), S.468 ff.).
Der Überschuss per t=1 beträgt dann 90 €
1 (Zeile 5), was auf die Lagerinvestition in t=0 von 200 €
0 bezogen werden kann. Die GMRoI beträgt gemäß Zeile 6 dann 45% p.a. Wenn die Nettoumsätze aber erst ein halbes Jahr später zu Zahlungen werden (also in t= 1,5), muss bei den Einzahlungen im zweiten Teil der Abb. 1 um ein halbes Jahr abgezinst werden (Division durch 1,10,5), so dass sich der Wert per t=1 auf 190,69 €
1 beläuft (Zeile 10). Dann darf wieder der GMRoI zu 40,3% berechnet werden.
Somit lässt sich festhalten, dass die Größen des Gross Profit zunächst hinsichtlich ihres zeitlichen Anfalls genauer untersucht werden müssen. Die Ergebnisse können sich bei fehlender Korrektur stark von den wirklichen unterscheiden. Ein weiteres Argument spricht für die einheitliche Definition der Renditen. Wenn das Kapital der Unternehmen knapp ist, dann sollte die Auswahl der
Handlungsmöglichkeiten nach Maßgabe der Kapitalrenditen erfolgen. Dies gilt dann nicht nur für Produkte, sondern auch für Investitionen in anderen Bereichen.
3. Probleme bei den Nettoumsätzen und Cogs
Die dargestellten Formeln erfordern bei den Umsätzen einige Präzisierungen. Insbesondere sei darauf hingewiesen, dass der
Preis immer der Nettopreis sein muss, also
ohne Umsatzsteuer und nach Berücksichtigung aller
Rabatte (in der Rechnung, auf den Rechnungsbetrag und Rückvergütungen). Zudem dürfen die Effekte der
Zahlungsziele (vgl. Varnholt/Lebefromm/Hoberg, S. 126-128) nicht vergessen werden. In der Literatur wird die Wirkung der verschiedenen Rabatte
price waterfall bezeichnet (vgl. Vohra/Krishnamurthi, S. 74 ff.), wobei in der Realität noch mehr
Erlösreduktionen anfallen. Es fehlen z. B. die Nachteile aufgrund von subventionierten Krediten, wozu auch eine
Nullprozentfinanzierung gehören kann.
Auch sind viele Elemente, die zurzeit in der Handelsförderung abgerechnet werden, eher den Rabatten zuzuordnen als den Marketingkosten, weil die Handelspartner nicht selten darauf bestehen, die Handelsförderung von den abgenommenen Mengen abhängig zu machen. Solche
Marketingkosten müssten dann eigentlich im Gross Profit abgebildet werden. Wichtig ist zu erkennen, dass der
Gross Profit üblicherweise auf Basis des
externen Rechnungswesens ermittelt wird, während der
Deckungsbeitrag dem
internen Rechnungswesen zuzuordnen ist. Bei ihm bestehen wesentlich mehr Freiheiten, um die betriebswirtschaftliche Realität angemessen abbilden zu können. Ob diese von den Unternehmen richtig genutzt werden, ist eine andere Frage.
Im Folgenden wird der Umsatz daher als Nettoumsatz nach
Kapitalkosten UN (und der Preis als
Nettopreis pN) angegeben, um deutlich zu machen, dass wirklich alle Erlösschmälerungen inklusive eventueller Finanzierungskosten abgezogen sein müssen. Zudem sei auf die Notwendigkeit hingewiesen, die zu betrachtende Periode genau festzulegen. Denn die Wirkungsbeziehungen können sich schon wenig später ändern, was insb. für Produkte gilt, deren Nachfrage saisonal schwankt.
Bei den Cogs wurde bereits darauf hingewiesen, dass der
Einbezug der Fixkosten in eine kurzfristige Steuerungsgröße nicht akzeptabel. Was dabei passieren kann, möge das folgende wieder sehr vereinfachte Beispiel in Abb. 2 zeigen, das mit und ohne Fixkosten gerechnet wird.
Produkt 1 weise in den laufenden Auszahlungen von -150 €
0 fixe Bestandteile in Höhe von -50 €
0 auf (Zeile 1). Um diesen Wert sind die
Auszahlungen im zweiten Tel verringert (Zeile 7), wenn ohne Fixkosten gerechnet wird. Im oberen Teil der Abb. 2 wird werden die laufenden Ein- und Auszahlungen auf das Ende der Laufzeit (hier t=1) hochgezinst. Der Saldo von 39,88 €
1 (Zeile 5) kann dann auf das eingesetzte Kapital von 200 €
0 bezogen werden, so dass sich der der GMRoI mit Fixkosten zu 19,9 % ermitteln lässt.
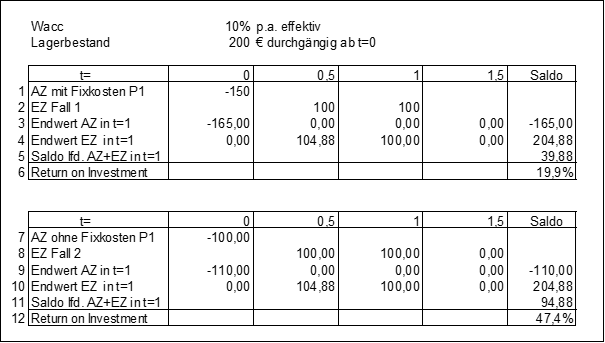 Abb. 2: Produkt 1 mit und ohne Fixkosten
Abb. 2: Produkt 1 mit und ohne Fixkosten
Ohne die
nicht entscheidungsrelevanten fixen Kosten steigt die Rendite wesentlich an, was dem zweiten Teil der Abb. 2 zu entnehmen ist. Nun sei ein zweites Produkt mit einer ähnlichen Zahlungsstruktur betrachtet. Es weist geringere Auszahlungen in Zeile 1 der Abb. 3 auf. Da die Einzahlungen unverändert sind, steigt dadurch die Rendite von 19,9 % bei Produkt 1 auf 25,4 % bei
Produkt 2. Aber es sei angenommen, dass die anteiligen Fixkosten mit –20 €
0 viel geringer seien.
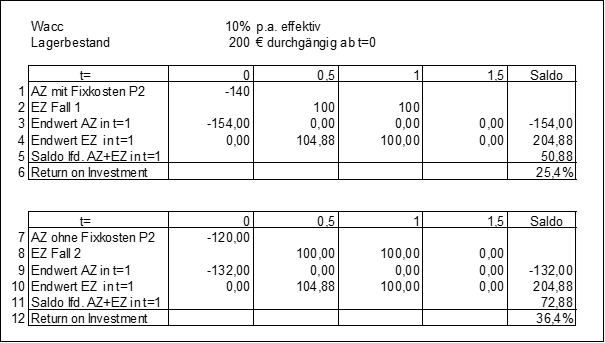 Abb. 3: Produkt 2 mit und ohne Fixkosten
Abb. 3: Produkt 2 mit und ohne Fixkosten
Durch die geringeren fixen Elemente in Zeile 7 der Abb. 3 steigt die Rendite viel geringer, nämlich nur auf 36,4%, was jetzt unter der Rendite von Produkt 1 liegt.
Die Verwendung der Gross Profits kann somit zu falschen Entscheidungen führen.
4. Verbesserte Kenngrößen
Wenn es um
kurzfristige Entscheidungen geht, sollten
Deckungsbeitragsrechnungen eingesetzt werden, die genau auf die Besonderheiten des Unternehmens zugeschnitten werden können. Denn sie gehören zum internen Rechnungswesen, das nur geringen Beschränkungen unterliegt. Allerdings ist an die oben erwähnten Anwendungsvoraussetzungen zu denken, dass z. B. die Nettoumsätze und die variablen Kosten linear verlaufen. Zusätzliche Rabatte sind da nicht vorgesehen, bzw. es müssten fallweise Erweiterungen vorgenommen werden (vgl. auch Atrill/McLaney, S. 82 ff.). Auf Basis der Deckungsbeiträge können Produkte, Geschäftsbereiche, Regionen, Kunden(gruppen) usw. analysiert werden (vgl. z. B. Gallo, HBR 2017, S. 1 ff.).
Im konkreten Fall sollte die
Deckungsspanne d eingesetzt werden als Differenz aus
Nettopreis pN und den
variablen Stückkosten kv. Der Deckungsbeitrag einer Periode ergibt sich dann als Produkt der
Deckungsspanne d und der Menge in dieser Periode. Wenn dann Engpässe zu berücksichtigen sind, so bieten sich relative Deckungsspannen an, um z. B. die Beanspruchung des Lagers abbilden zu können. Dabei kann dann entweder das
gebundene Kapital den Engpass darstellen oder der benötigte Platz, der zum Beispiel in Paletten gemessen werden kann oder allgemeiner in Kapazitätseinheiten. Im letzten Fall sieht die
relative Deckungsspanne drel wie folgt aus:
d
rel = d / PK in €/KE
|
drel
|
Relative Deckungsspanne in €/KE
|
|
d
|
Absolute Deckungsspanne: pN – kv in €/ME
|
|
PK
|
Produktionskoeffizient in KE/ME
|
Wie oben dargestellt müssen die Größen auf den gleichen Zeitpunkt bezogen sein, was in der
Kosten- und Leistungsrechnung üblicherweise die Periodenmitte ist. Das Produkt mit der höchsten relativen Deckungsspanne wird dann bevorzugt. Alternativ zur relativen Deckungsspanne kann auch der
Periodendeckungsbeitrag durch die Periodenmengen dividiert werden. Wichtig ist in beiden Fällen, dass die Größen nur kurze Zeit gültig sind und häufig neuberechnet werden müssen, wenn sich Daten ändern.
Somit
dürfen Deckungsbeiträge (absolute und relative) nur für kurzfristige Fragestellungen eingesetzt werden. Schon wenn sich der benötigte Lagerbedarf für ein Produkt ändert, muss neu gerechnet werden.
Dies gilt insb. für Produkte, deren Absatz eine hohe Saisonabhängigkeit aufweist. Sobald Änderungen in der Kapazität (hier z. B. Lagerkapazität) auftreten bzw. geplant werden, sollten mehrjährige Analysen verwendet werden. Hier gibt es mit den Vollständigen Finanzplänen ein gutes Werkzeug (vgl. hierzu z. B. Varnholt/Hoberg/Gerhards/Wilms, S. 55 ff.).
5. Schlussfolgerung
Die vorgeschlagene
Steuerungsgröße GMRoI ist mit vielen Problemen beladen. Selbst wenn ein Teil der Probleme gelöst wurde, hilft die Größe nur in wenigen Sonderfällen, Zudem ist sie nicht gut greifbar und wenig verständlich.
Nur wenn der Lagerbestand einen Engpass darstellt, sollte man die Größe GMRoI in Betracht ziehen. Dabei ist dann aber anzumerken, dass der Engpass finanzieller Art sein muss. Der wohl häufigere Fall, dass ein mengen- bzw. gewichtsbezogener Engpass vorliegt, wird von der Größe nicht betrachtet. Hier sollte die bewährte
Deckungsbeitragsrechnung eingesetzt werden. In der Variante der relativen Deckungsspannen kann ein gemeinsamer Engpass wie z. B. der der Lagerkapazität optimal bewirtschaftet werden.
letzte Änderung P.D.P.H.
am 25.04.2024
Autor:
Dr. Peter Hoberg
Bild:
Bildagentur PantherMedia / Olivier26
|
Autor:in
 |
Herr Prof. Dr. Peter Hoberg
Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung.
|
|
weitere Fachbeiträge des Autors
| Forenbeiträge
|










 Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT.
Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT. Wie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.
Wie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.  Viel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.
Viel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.
 Die Stadt Weinheim mit rund 45.000 Einwohner*innen ist innerhalb der Metropolregion Rhein-Neckar ein beliebter Wohnort mit großem Bildungs-, Sport- und Kulturangebot. Wir als Beschäftigte (ca. 800) der Stadtverwaltung wollen unsere Stadt Tag für Tag weiterentwickeln. Wenn Sie Teil un... Mehr Infos >>
Die Stadt Weinheim mit rund 45.000 Einwohner*innen ist innerhalb der Metropolregion Rhein-Neckar ein beliebter Wohnort mit großem Bildungs-, Sport- und Kulturangebot. Wir als Beschäftigte (ca. 800) der Stadtverwaltung wollen unsere Stadt Tag für Tag weiterentwickeln. Wenn Sie Teil un... Mehr Infos >>
 Unsere ausgeprägte Leidenschaft für Live Entertainment, Musicals und Theateraufführungen auf höchstem Niveau ist, was uns bei Stage verbindet. Diese gemeinsame Begeisterung macht aus den vielfältigsten Mitarbeitenden in unterschiedlichsten Jobs ein hingebungsvolles Team: ein echtes „Wir“. Und das... Mehr Infos >>
Unsere ausgeprägte Leidenschaft für Live Entertainment, Musicals und Theateraufführungen auf höchstem Niveau ist, was uns bei Stage verbindet. Diese gemeinsame Begeisterung macht aus den vielfältigsten Mitarbeitenden in unterschiedlichsten Jobs ein hingebungsvolles Team: ein echtes „Wir“. Und das... Mehr Infos >>
 Die WHU – Otto Beisheim School of Management ist die renommierteste private Hochschule in Deutschland und genießt auch international hohes Ansehen. Unsere Standorte in Vallendar und Düsseldorf bieten ein spannendes und sehr internationales Arbeitsumfeld. Die Kultur an der WHU ist geprägt von unte... Mehr Infos >>
Die WHU – Otto Beisheim School of Management ist die renommierteste private Hochschule in Deutschland und genießt auch international hohes Ansehen. Unsere Standorte in Vallendar und Düsseldorf bieten ein spannendes und sehr internationales Arbeitsumfeld. Die Kultur an der WHU ist geprägt von unte... Mehr Infos >>
 Die Stadtwerke Heilbronn GmbH ist ein wachstumsorientiertes Infrastruktur- und Dienstleistungsunternehmen. Mit 400 Mitarbeitern erbringen wir Leistungen für die Einwohner der Stadt Heilbronn und die in Heilbronn ansässigen Unternehmen in den Bereichen Wasserversorgung, Stadtbahn und -bus, Eis... Mehr Infos >>
Die Stadtwerke Heilbronn GmbH ist ein wachstumsorientiertes Infrastruktur- und Dienstleistungsunternehmen. Mit 400 Mitarbeitern erbringen wir Leistungen für die Einwohner der Stadt Heilbronn und die in Heilbronn ansässigen Unternehmen in den Bereichen Wasserversorgung, Stadtbahn und -bus, Eis... Mehr Infos >>
 Die Energie Südbayern (ESB) bildet gemeinsam mit den Tochterunternehmen Energienetze Bayern und der ESB Wärme die ESB-Unternehmensgruppe. Mit rund 450 Mitarbeiterinnen und Mitarbeitern, Auszubildenden und Trainees stehen wir für leistungsfähigen Service, flexible Energiepr... Mehr Infos >>
Die Energie Südbayern (ESB) bildet gemeinsam mit den Tochterunternehmen Energienetze Bayern und der ESB Wärme die ESB-Unternehmensgruppe. Mit rund 450 Mitarbeiterinnen und Mitarbeitern, Auszubildenden und Trainees stehen wir für leistungsfähigen Service, flexible Energiepr... Mehr Infos >>
 Die SVG Straßenverkehrsgenossenschaft Berlin und Brandenburg eG ist eine von derzeit 15 Straßenverkehrsgenossenschaften im gesamten Bundesgebiet. Als rechtlich und wirtschaftlich selbständige Genossenschaft sind wir ein Mitgesellschafter der SVG Zentrale in Frankfurt am Main. Sie bündelt und... Mehr Infos >>
Die SVG Straßenverkehrsgenossenschaft Berlin und Brandenburg eG ist eine von derzeit 15 Straßenverkehrsgenossenschaften im gesamten Bundesgebiet. Als rechtlich und wirtschaftlich selbständige Genossenschaft sind wir ein Mitgesellschafter der SVG Zentrale in Frankfurt am Main. Sie bündelt und... Mehr Infos >>
 Sie übernehmen als kaufmännischer Leiter (m/w/d) die Verantwortung für die Führung Ihres Teams und unterstützen den Geschäftsführer der Lorenz GmbH & Co. KG bei allen betriebswirtschaftlichen Fragen zur Steuerung des Unternehmens. Fachlich berichten Sie an die in München ansässige BRUNATA... Mehr Infos >>
Sie übernehmen als kaufmännischer Leiter (m/w/d) die Verantwortung für die Führung Ihres Teams und unterstützen den Geschäftsführer der Lorenz GmbH & Co. KG bei allen betriebswirtschaftlichen Fragen zur Steuerung des Unternehmens. Fachlich berichten Sie an die in München ansässige BRUNATA... Mehr Infos >>
 Techtronic Industries ist weltweit führend in der Herstellung und im Vertrieb von hochwertigen Elektrowerkzeugen für den DIY-Markt und den Profieinsatz sowie von Gartengeräten. Ein strategischer Fokus auf leistungsstarke Marken, innovative Produkte und außergewöhnliche Menschen bestimmt unseren E... Mehr Infos >>
Techtronic Industries ist weltweit führend in der Herstellung und im Vertrieb von hochwertigen Elektrowerkzeugen für den DIY-Markt und den Profieinsatz sowie von Gartengeräten. Ein strategischer Fokus auf leistungsstarke Marken, innovative Produkte und außergewöhnliche Menschen bestimmt unseren E... Mehr Infos >>







 Tipps, Charts und Diagramme für Ihre tägliche Arbeit mit Microsoft Excel® im Controlling. Präsentiert von Controlling-Portal.de. Sogenannte Dashboards werden heute vom Management erwartet. Möglichst auf einem Blatt sollen alle wichtigen Kennzahlen auf einem Blick erfassbar sein.
Tipps, Charts und Diagramme für Ihre tägliche Arbeit mit Microsoft Excel® im Controlling. Präsentiert von Controlling-Portal.de. Sogenannte Dashboards werden heute vom Management erwartet. Möglichst auf einem Blatt sollen alle wichtigen Kennzahlen auf einem Blick erfassbar sein.
 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>