Controllers Trickkiste: Wachstumsraten und ihre Fallen

Bei der Analyse von Sachverhalten ist es häufig interessant, Entwicklungen im Zeitablauf zu zeigen. Neben den absoluten Zahlen (z. B. der Umsatz im Jahre 2020) interessieren auch ihre Änderungen von Jahr zu Jahr. Da die Zahlen unterschiedliche Größenordnungen – z. B. bei Umsatz und Gewinn - aufweisen können, ist es häufig hilfreich, die Änderungen zu normieren, indem man sie auf den Ursprungswert bezieht. Dies ergibt dann die Wachstumsraten. Im folgenden Beispiel sind die einjährigen Wachstumsraten für Umsätze und Gewinne eines Unternehmens angegeben (s. Tabelle 1).


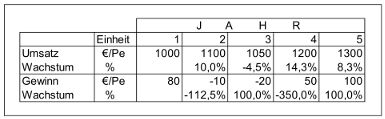Tabelle 1

Die Umsätze und Gewinne tragen die Einheit €/Pe, was bedeutet, dass sie in Euro gemessen werden. Zeitlich fallen sie durchschnittlich zur Mitte der betrachteten Periode an. Während die erste Wachstumsrate mit 10 % noch leicht nachzuvollziehen ist, weil sie sich auf 1000 €/Pe als Basiswert bezieht, sind die anderen Raten hilfreich. Hingegen können die Wachstumsraten des Gewinns auf den ersten Blick erstaunen und sogar in die Irre führen, was im Folgenden untersucht werden soll.

2. Einjährige Wachstumsraten

Definition
Gerade im Controlling werden häufig aktuelle Größen mit denen des Vorjahrs (= Basiswert) verglichen oder bei der Planung die Planwerte mit den aktuellen Werten. Dafür benötigt man die einjährige Wachstumsrate WR, für welche die folgende Formel gilt:

WR  =  (NW – BW)/BW

• WR: Wachstumsrate
• NW: Neuer Wert
• BW: Basiswert

Oder noch einfacher, indem die Differenz durch den Basiswert BW dividiert wird:

WR  = NW/BW - 1

Die erste Wachstumsrate ergibt sich konkret zu:

WR₁   = 1100/1000 – 1 = 1,1 – 1 = 0,1 = 10%

Das Ergebnis beträgt also dezimal 0,1 oder prozentual 10%.

Nur am Rande sei erwähnt, dass in vielen Lehrbüchern eine Multiplikation mit 100 vorgenommen wird, um zu den Prozentwerten zu gelangen. Das ist jedoch falsch, weil "%" ja pro Hundert heißt. Bei der Prozentangabe findet somit nur eine Erweiterung um 100/100 statt, wobei der Nenner durch das Prozentzeichen abgebildet wird. 10 % heißt somit 10 pro 100 = 0,1.

Problemfälle
Während die Wachstumsraten der Umsätze in der obigen Tabelle gut nachzuvollziehen sind, gilt dies nicht für das Wachstum der Gewinne. In Periode 2 wird ein Wert von -112,5 % ausgewiesen. Dies bedeutet, dass nicht nur der gesamte Gewinn verloren gegangen ist (also 100 %), sondern sogar ein Verlust von -10 €/Pe entstanden. Mit dieser Interpretation ist die Wachstumsrate betriebswirtschaftlich richtig zu verstehen.

Dies ist in der Folgeperiode 3 nicht mehr der Fall. Der Verlust hat sich von -10 €/Pe auf -20 €/P verdoppelt. Mathematisch korrekt wird dafür +100% ausgewiesen:

-20/-10 -1 = 1 = 100 %

Inhaltlich sieht es so aus, als hätte das Management mit einer Gewinnverdoppelung einen guten Job gemacht. Tatsächlich wurde aber der Verlust verdoppelt. In so einem Fall muss der Controller unbedingt aufzeigen, dass die 100% nicht positiv sind. Beispielsweise könnte ein "w" für worse angehängt werden: 100% w. Die entsprechende "Wenn-Bedingung" kann leicht im Excel hinterlegt werden.

Genauso irreführend ist die nächste Wachstumsrate des Gewinns von Jahr 3 auf Jahr 4:

+50/-20-1 = -3,5 = -350 %

Sie legt eine katastrophale Performance des Unternehmens nahe. Aber auch in diesem Fall stimmt es nicht, weil das Unternehmen ja aus den roten Zahlen herausgekommen ist, was sicher eine positive und nicht eine negative Änderung darstellt. Es kann also festgehalten werden, dass immer dann Probleme auftauchen, wenn der Basiswert, der ja im Nenner steht, negative Werte aufweist.

Ebenfalls problematisch kann es werden, wenn der Gewinn im Basisjahr den Wert Null annimmt. Es kommt dann zu einer Division durch Null, was zu einem Fehler führt. Mathematisch führt ein positiver Gewinn nach einem Wert von 0 zu einem unendlich hohen Wachstum. Dies ist der Extremfall des Problems, dass tolle Wachstumsraten leicht erreicht werden können, wenn die Basiswerte sehr niedrig sind.

Bei einem Wert von 0 würde sich sogar ein unendlich hohes Wachstum ergeben. Somit ist entweder das Unendlich Zeichen “∞“ einzusetzen oder ein Hinweis, dass in diesem Fall ein Ausweis wenig sinnvoll ist. Teilweise kann man auch mit einem “+“ oder “-“ einen ersten Hinweis geben, wie die Änderung einzuschätzen ist. Auch diese Kennzeichnungen lassen sich einfach mit Excel-Formeln umsetzen.

Prozentpunkte
Häufig ist es interessant, auch die Änderungen relativer Werte auszuweisen. Im obigen Beispiel könnte man die Entwicklung der Umsatzrenditen als Verhältnisse von Gewinn und Umsatz analysieren. Dadurch ergibt sich die Tabelle 2:


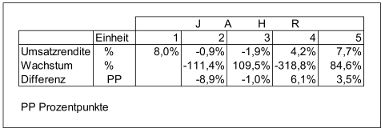Tabelle 2

Wenn man jetzt die Änderung angeben will, ist die Wachstumsrate häufig nicht geeignet. Neben den oben erwähnten Problemen der Werte im Basisjahr kommt noch hinzu, dass die Werte bei solchen Relationen häufig klein sind, so dass die prozentualen Änderungen extrem ausschlagen. Die Zeile "Wachstum" in der obigen Tabelle zeigt das deutlich. Besser kann es sein, die Differenz der relativen Größen – hier der Umsatzrenditen – zu ermitteln. Sie zeigen sehr gut, ob sich die Profitabilität verbessert oder verschlechtert hat. Im Jahr 3 bedeutet die -1,0 % PP, dass ein Prozentpunkt Umsatzrendite verloren wurde. In vielen Jahresabschlüssen hat es sich bereits eingebürgert, solche Rechnungen mit "pp" für Prozentpunkte auszuweisen.

Mehrjährige Wachstumsraten

Wenn eine Entwicklung über mehrere Jahre dargestellt werden soll, so wird häufig die durchschnittliche jährliche Verzinsung ermittelt. Auch in deutschen Unternehmen findet man fast immer den amerikanischen Begriff CAGR (compounded annual growth rate). Gesucht wird das durchschnittliche jährliche Wachstum vom Basiswert BW in t=1 bis zum Wert des letzten Jahres, was im Beispiel t=5 ist. Die dazu notwendige Formel lautet:

CAGR = (WLJ/BW)^(1/(tn-1)) – 1

• CAGR: Jährliche durchschnittliche Wachstumsrate
• WLJ: Wert im letzten Jahr
• tn:  Anzahl der Perioden

Bei einer fünfjährigen Planung wird somit die vierte Wurzel aus dem Verhältnis vom Wert im letzten Jahr zum Basiswert BW gezogen. Als Beispiel mögen die Zahlen in Tabelle 3 vorliegen:


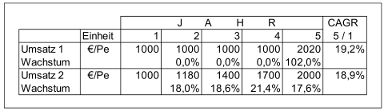Tabelle 3

Für das durchschnittliche jährliche Wachstum des Umsatzes der Produktgruppe 1 ergibt sich:

CAGR₁ = (2020/1000)^0,25 -1 = 1,192 - 1 = 0.192 = 19,2% p.a. 

Bei den vorliegenden 5 Perioden (tn=5) muss also die vierte Wurzel gezogen werden. Genauso wird das durchschnittliche jährliche Wachstum für den Umsatz 2 ermittelt. Da der Umsatz in Jahr 5 etwas niedriger ist, ergibt sich eine Durchschnittsrendite von 18,9% pro Jahr. Damit ist das Wachstum der Produktgruppe 1 auf den ersten Blick höher.

Ein Problem aber besteht darin, dass die Entwicklung in den Zwischenjahren nicht berücksichtigt wird. Während die Produktgruppe 2 ein ziemlich gleichmäßiges Wachstum aufweist, passiert in der Umsatzgruppe 1 im letzten Jahr ein "Wunder". Nach 4 Jahren mit Nullwachstum explodiert der Umsatz.

In der Praxis wird nicht selten mit solchen Effekten getrickst, weil die entscheidenden Wachstumsraten erst in vielen Jahren kommen müssen, wenn die verantwortlichen Manager schon längst einen anderen Job haben. Hier muss der Controller sehr kritisch nach den Gründen fragen. Man sollte den CAGR also nie isoliert betrachten.

Missbrauch von Wachstumsraten

Jedes Unternehmen zeigt gerne positive Wachstumsraten, insbesondere bei Gewinngrößen. Die Definition der Gewinne war in den obigen Beispielen unterblieben, weil dies im Kontext der Wachstumsraten nicht relevant war. Anders sieht es im Reporting der Unternehmen aus. Hier gibt es eine große Auswahl von Gewinngrößen. Es geht mit dem Rohertrag los (nur Materialkosten abgezogen) über viele weitere Stufen bis schließlich zum EVA (economic value added), bei dem alle betriebswirtschaftlich relevanten Effekte berücksichtigt sind (sein sollten). Dazu kommen jede Menge pro Forma Kalkulationen, mit denen Sondereffekte eliminiert werden sollen, was insbesondere dann angewandt wird, wenn die aktuellen Wachstumsraten nicht gut genug aussehen.

Wenn somit nur Wachstumsraten einiger ausgewählter Überschussgrößen in Unternehmensmitteilungen ausgewiesen werden, sollte das den Verdacht des Lesers erwecken. Nicht selten wird man herausfinden, dass das Gesamtbild gar nicht so gut aussieht wie es die ausgewählten Wachstumsraten erscheinen lassen.

Empfehlungen

Um Probleme zu vermeiden, sollte der Controller folgende Tipps beachten:

1. Wann immer das Basisjahr einen negativen Wert aufweist, darf die resultierende Wachstumsrate nicht ohne Anmerkung (z. B. "w" für worse) verwendet werden.
2. Sollte das Basisjahr (z. B. der Gewinn) einen Wert von 0 haben, läuft die Wachstumsrate auf einen Fehler (Division durch 0). Das muss abgefangen werden. Entweder durch ein "n. a." oder durch ein "∞".
3. Wachstumsraten von Anteilen sollten in Prozentpunkten angegeben werden.

P.S.: Der Tipp zum Angeben

In langfristigen Planungen wird häufig gefragt, wie lange es dauert, bis sich eine Größe verdoppelt hat. Wenn der Controller die 72er Regel kennt, kann er schnell gute Abschätzungen durchführen. Diese Regel besagt, dass eine Verdopplung dann stattfindet, wenn das Produkt aus Wachstumsrate und Laufzeit 72 beträgt.

Als Beispiel sei angenommen, dass über 9 Jahre geplant werden soll. Dann beträgt die notwendige Wachstumsrate 72/9 = 8%. Tabelle 4 mit der korrekten Kalkulation zeigt, dass diese Kombination mit 1,999 praktisch eine Punktlandung erzeugt. Erstaunlich ist, dass die Verdopplung für einen sehr weiten Bereich von Wachstumsraten und Laufzeitjahren in guter Näherung funktioniert.


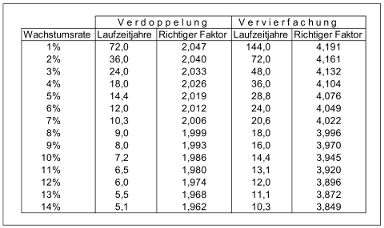Tabelle 4

Nicht mehr ganz so passend aber immer noch gut ist die 144er Daumenregelung für eine Vervierfachung der Werte. Die längeren Laufzeiten sorgen durch die Exponentialfunktion für etwas größere Abweichungen. Wer diese Daumenregeln im Kopf hat, kann schnell beurteilen, ob eine Kombination von Wachstumsrate und Laufzeitjahren in etwa passt.

Aktuelles Beispiel für die falsche Verwendung von Wachstumsraten

Die Entwicklungen der Künstlichen Intelligenz (KI) haben inzwischen dazu geführt, dass immer mehr Anwendungen sichtbar werden, die mithilfe der Programme rationalisiert werden können. Insofern wird von riesigen Wachstumsraten in den nächsten Jahren ausgegangen. 

Im Teilbereich der generativen KI (ChatGPT, Jasper Chat, Google Bard usw.) soll der Jahresumsatz von aktuell 40 Mrd$ in 2022 auf 1300 Mrd$ in 2032 steigen (vgl. Bloomberg 1.6.2023). Das wäre für alle Marktteilnehmer extrem interessant ist. Alle großen Internet- Unternehmen wollen dabei sein, um ihr Stück vom gewaltigen Kuchen zu bekommen.

Wie sehen jetzt die möglichen Wachstumsraten aus? Einmal könnte man das Gesamtwachstum über die gesamten 10 Jahre angeben, was zu folgender Rate führt: 1300/40– 1 = 3150%, eine Zahl, unter der sich kaum jemand etwas vorstellen kann. Also ist es sinnvoll, diese Rate zur besseren Verständlichkeit auf ein jährliches Wachstum herunterzubrechen.

Eine einfache Division durch die Anzahl der Jahre würde 315% ergeben, was auch nicht sinnvoll erscheint.

Erst mit der CAGR als jährlicher Wachstumsrate kommt man zu einer handhabbaren Größe, die (1300/40)(1/10) = 42% beträgt. 

Dies stellt ein enormes jährliches Wachstum dar, was sich auch darin zeigt, dass sich der Umsatz alle 2 Jahre verdoppelt.

Die Zahlen des Beispiels belegen, dass die Unterscheidung zwischen Gesamtwachstum über 10 Jahre bzw. jährlichem Wachstum essenziell ist. Auch muss dargelegt werden, ob die Jahresverzinsung linear oder „compounded“ gerechnet wurde.

Die Präzision ist gerade bei großen Wachstumsraten wichtig, weil der linear denkende Mensch mit Exponentialfunktionen wie im CAGR nicht gut klar kommt.

Im obigen Fall wurde daher in einem Beitrag eine Wachstumsrate von 42% zitiert, ohne darzulegen, dass es sich um eine jährliche compounded Rate handelte.

Schlussbemerkung

Mit Wachstumsraten kann der Controller Entwicklungen noch besser verstehen und dann auch die dahinter liegenden Sachverhalte erklären. Voraussetzung ist aber auch für den Controller, dass sie korrekt bestimmt werden. Zudem zeigen sie als relative Größe nur einen Teil der Wirklichkeit. Hohe Steigerungsraten bei einer geringen Basis führen in die Irre. Im Weiteren ist es entscheidend, die Einheiten richtig anzugeben. Im einfachsten Fall z. B. einer Zeitreihe muss klar sein, ob es sich um monatliche, quartalsweise oder jährliche Wachstumsraten handelt.

Auch Zinssätze sind Wachstumsraten. Hier können Missverständnisse vermieden werden, wenn für die Verzinsungen angegeben werden, wann sie starten und wann sie enden (vgl. zu dieser exakteren Erfassung des Zeitaspektes Hoberg (2018), S. 468 ff.). 

Der Controller muss somit doppelt aufpassen. Einmal, dass er selbst sauber arbeitet (nobody is perfect) und zum anderen, dass er eventuelle Probleme aufdeckt. Bei letzteren ist zu unterscheiden, ob sie auf Unfähigkeit, Unachtsamkeit oder Absicht begangen werden. Gerade die ausschließliche Nennung von Prozenten sollte den Verdacht der Manipulation wecken.

Insofern sollte der erfahrene Controller Wachstumsraten immer nur als zusätzliche Information einsetzen bzw. akzeptieren. Die absoluten Zahlen müssen auf jeden Fall genannt werden. Bei mehrjährigen Prozessen reicht die Nennung der durchschnittlichen jährlichen Wachstumsrate (CAGR) nur im ersten Schritt, weil die Entwicklungen innerhalb der Jahre sehr unterschiedlich sein können. 

Erst auf Basis des Gesamtbildes kann eine qualifizierte Beurteilung erfolgen.


Literaturhinweise:

• Bloomberg:  Generative AI to become a 1.3-trillion Market by 2032, in: https://www.bloomberg.com/company/press/generative-ai-to-become-a-1-3-trillion-market-by-2032-resear..., 1.6.2023.

Quelle: panthermedia.net / Rijal Muttaqin letzte Änderung P.D.P.H. am 03.06.2025 Autor:  Dr. Peter Hoberg

Autor:in

	Herr Prof. Dr. Peter Hoberg Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung.
weitere Fachbeiträge des Autors | Forenbeiträge